Nel precedente articolo (per maggiori informazioni leggi: Come misurare il rischio a ribasso (o Downside Risk) con Excel? Scopriamolo!) è stato spiegato come misurare il rischio al ribasso di un investimento in un fondo quando la deviazione standard non misura bene la dispersione dei rendimenti se non usata in tandem con altre metriche. In tale sede si vuole spiegare invece come calcolare il rischio di un asset relativamente ad un altro benchmark (covarianza, correlazione, CAPM come regressione, Alpha di Jensen, Tracking Risk).
Un target della misurazione del rendimento è determinare se il manager ha aggiunto valore sul benchmark (ossia il parametro preso a riferimento). È possibile quantificare la porzione dei rendimenti che possono essere attribuiti alle attività del manager di portafoglio isolando il valore aggiunto al fondo dai rendimenti assoluti lungo il periodo analizzato. In questo sede vedremo i modi per misurare questi rischi relativi al benchmark.
Osservazione 1> Data la relazione tra il rischio e il rendimento, si deve analizzare anche il livello di rischio del portafoglio che differisce dal benchmark. Molte volte il benchmark scelto guida il livello di rischio atteso nella strategia e, se questo fosse stabilito basandosi sulla volontà di rischiare dell’investitore e sulla combinazione del fondo che si sta valutando con le altre azioni nel portafoglio dell’investitore, è il rischio del fondo in relazione a quello del benchmark che noi siamo interessati a calcolare. Se il fondo fosse più rischioso del benchmark, allora ci aspetteremo rendimento più alti. Spesso il manager stabilirà una fascia attesa di rischio relativo del benchmark.
Il rischio si misura periodicamente per assicurare che rimanga all’interno di limiti accettabili. Se il fondo fosse meno rischioso del benchmark, il manager eviterebbe i rischi che sono richiesti per ottenere gli obiettivi a lungo termine dell’investitore.
Osservazione 2> Dalla prospettiva del manager, è il rendimento relativo del benchmark, il rischio relativo del benchmark e il rendimento corretto per il rischio che ci permettono di misurare la nostra performance. Quindi sia gli investitori sia i portfolio manager sono interessati a misurare il grado dei rischi relativi al benchmark presi in riferimento al rendimento relativo del benchmark.
Quando il rischio assoluto è approssimato dalla deviazione standard dei rendimenti, il rischio relativo viene misurato guardando a come i rendimenti dei fondi e i rendimenti di benchmark variano insieme:
- Se il fondo e il benchmark si muovono su e giù insieme, ci sarà un grado di rischio assoluto, come misurato dalla deviazione standard, ma non ci sarà nessun rischio relativo.
- Se il rendimento del fondo e del benchmark variassero in modi differenti, ad esempio se i rendimenti del fondo fossero generalmente più negativi del benchmark qualora il mercato fosse in ribasso, allora il fondo avrà un maggior grado di rischio relativo del benchmark rispetto a quello implicato dal benchmark. La variabilità delle differenze di rendimento periodico rispetto al benchmark misura il rischio specifico della strategia che si sta valutando.
Covarianza
Osservazione 3> Le misure che associano le serie storica dei rendimenti del fondo e del benchmark ci fanno comprendere quanto rischio relativo al benchmark viene esposto dal portafoglio. Le statistiche del rischio relativo al benchmark sono basate sul concetto di misurazione di quanto strettamente i rendimenti periodici del fondo varino rispetto ai rendimenti del benchmark.
Possiamo dare un senso a come i fondi varino insieme, usando una grafico che tracci la sequenza dei rendimenti mensili, come nello schema 11.1.
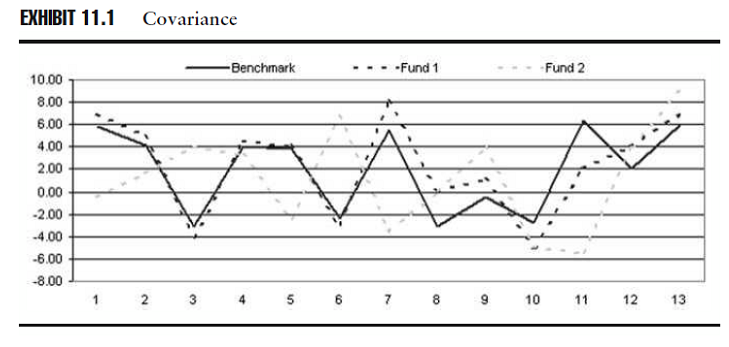
Fonte: Investment Performance Measurement (Bruce J. Feibel)
Qui abbiamo un benchmark e due portafogli. Possiamo vedere che i rendimenti del fondo 1 generalmente si muovono su e giù rispetto al benchmark: I rendimenti del fondo 2 non si muovono in modo simile al benchmark, difatti, il fondo 2 spesso si muove nelle direzioni opposte rispetto ai rendimenti del benchmark.
Osservazione 4> Noi siamo interessati a quantificare questo grado di covariabilità, o covarianza. La covarianza è una misura statistica della tendenza di due serie di dati di muoversi insieme e viene calcolata usando una serie di rendimenti di fondo e di benchmark. Essa misura la direzione e il grado di associazione dei rendimenti del fondo a quelli del benchmark, nonché l’ampiezza della variabilità negli stessi.
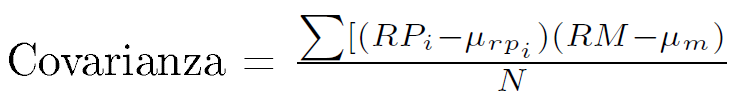
Procedimento operativo (ed esiste anche una built-in function per questo):
- Si calcola le differenze fra i rendimenti del fondo e la media dei fondi di rendimento e fra i rendimenti del benchmark e la media dei rendimenti del benchmark.
- Poi si moltiplicano insieme le differenze periodiche dalle due serie e
- si fa la somma dei prodotti delle due differenze.
- Infine, si calcola la media dividendo per il numero delle osservazioni periodiche.
Lo schema Excell dimostra il calcolo della covarianza del nostro fondo e del benchmark di riferimento, ossia 0,0013.
La covarianza è una statistica utile per misurare la portata della differenza nella variabilità tra le due serie di rendimenti. Lungo i rendimenti attesi dell’insieme degli asset in portafoglio, si usa la covarianza tra esse per determinare l’asset allocation ottimale. Infatti, in portafogli diversificati il grado di rischio del portafoglio approssimerà la covarianza media tra le azioni contenute nel portafoglio.
Possiamo utilizzare il foglio Excell per vedere come i rendimenti del fondo e del benchmark influenzino la covarianza.
Osservazione 5> Una covarianza totale positiva indica che le serie di rendimenti sono associate, ossia che si muovono insieme. Una covarianza negativa indica che esse si muovono in direzioni opposte. Ciò potrebbe essere un’interessante proprietà che un fondo dovrebbe avere a causa della sua varietà di benefici. Quando non esiste una relazione tra i rendimenti di fondo e di benchmark, i prodotti delle differenze mensili saranno a volte positivi e a volte negativi; calcolandone la media su tutto il periodo si produce una covarianza bassa o pari a 0.
Lo schema 11.3 riassume la spiegazione della covarianza.

Fonte: Investment Performance Measurement (Bruce J. Feibel)
Ossevazione 6> Il fondo ha una covarianza con un benchmark pari a 0,0013, ma che significa? La covarianza è difficile da interpretare come qualcosa di diverso rispetto al prodotto medio delle differenze tra le deviazioni di rendimento del fondo e del benchmark. La covarianza è anche difficile da usare nei confronti tra portafogli perché è influenzata dalla portata assoluta dei rendimenti.
Correlazione
Osservazione 7> Date le difficoltà nell’utilizzo della covarianza, è possibile standardizzarla convertendola in un coefficiente di correlazione, che è molto più utile per un confronto diretto. La correlazione è una misura della quantità secondo la quale due investimenti variano insieme. Essa misura la direzione e il grado di associazione nei rendimenti di fondo e di benchmark.
Per calcolare la correlazione, prima si calcola la covarianza fra i rendimenti del fondo e del benchmark. In seguito si divide la covarianza per la moltiplicazione fra le deviazioni standard del fondo e del benchmark, il quale ha un effetto di mettere in ordine di grandezza la covarianza in un’estensione tra 1 positivo e 1 negativo (consiglio: built-in function di Excel).
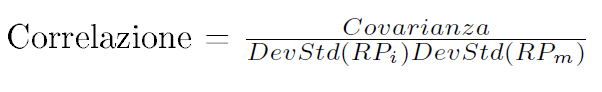
Osservazione 8> Una correlazione +1 indica che i rendimenti sono perfettamente correlati ma non indica che le serie di rendimenti sono le stesse. Per esempio, un fondo con rendimenti di ogni periodo che corrispondano esattamente al triplo di quelli del rendimento del benchmark del periodo, avrà una correlazione pari a 1. Un coefficiente di correlazione di -1 indica una perfetta correlazione negativa, che significa che i rendimenti del fondo si muovono in direzione proporzionale esattamente inversa al benchmark (-10% per fondo +30% per il benchmark). Le correlazioni possono essere usate per esaminare le relazioni tra il fondo e il suo benchmark, tra fondi differenti o tra benchmark differenti.
Il foglio Excell mostra anche il calcolo della correlazione del nostro fondo e del nostro benchmark pari a 0,88. Ciò significa che c’è una relazione positiva e forte tra le due serie di rendimenti ma c’è anche una qualche differenza nel modo in cui loro variano e, quindi, anche nel rischio relativo al parametro di riferimento.
Lo schema 11.4 sintetizza la spiegazione della correlazione.

Fonte: Investment Performance Measurement (Bruce J. Feibel)
Coefficiente di determinazione (R^2)
Ossevazione 9> Mentre è facile interpretare i coefficienti di correlazione che sono vicini agli estremi 1 e -1, è difficile comprendere a intuito le correlazioni che giacciono all’interno. Elevando al quadrato il coefficienti di correlazioni possiamo ricavare una statistica che è più facile da interpretare. Il quadrato del coefficiente di correlazione è chiamato coefficiente di determinazione, o R al quadrato, che rappresenta la proporzione della variabilità in rendimenti di fondo con la quale noi possiamo relazionarci, ossia con la variabilità dei rendimenti del benchmark. Essa misura il grado di associazione nei rendimenti di fondo e di benchmark. Noi interpretiamo R al quadrato come la proporzione della quantità del rischio di mercato del portafoglio rispetto al rischio totale. Esso può essere usato per determinare l’appropriatezza del benchmark usato per stimare e attribuire la performance del fondo. Un alto R quadro indica che il portafoglio e il benchmark sono probabilmente esposti a fattori di rischio similari che guidano o stanno guidando i rendimenti.
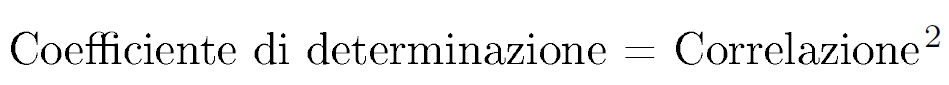
Lo schema 11.5 mostra il calcolo di R al quadrato del nostro fondo di riferimento, il quale è uguale a 0,78, indicando che il 78% della variazione del rendimento di fondo è relazionato con la variazione del rendimento di benchmark, mentre il 22% non lo è.
Osservazione 10> E’ chiamato coefficiente di non determinazione (complemento a 1 del coefficiente di determinazione) la percentuale di variazione di un rendimento di fondo non relazionato con la variazione del rendimento di benchmark.
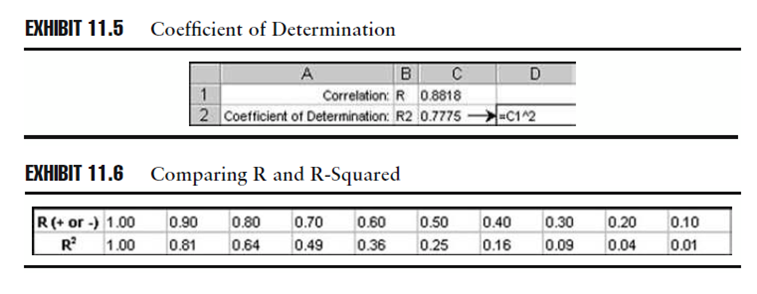
I valori di R al quadrato sono compresi tra 0 e 1. Un confronto del valore della correlazione e di R al quadrato illustra la ragione per cui R al quadrato è più facile da interpretare. Lo schema 11.6 mostra i valori di R al quadrato in vari livelli di correlazione. Notate quanto facilmente gli ‘alti’ valori della correlazione possano dare un’impressione sbagliata sulla proporzione della variabilità in rendimenti di fondo che sono realmente espressi nei rendimenti di benchmark.
Sembrerebbe che R al quadrato, la correlazione e la covarianza si duplichino reciprocamente come misure della variabilità relativa al benchmark. Infatti ogni statistica offre più informazioni della precedente:

Fonte: Investment Performance Measurement (Bruce J. Feibel)
Analisi di Regressione (CAPM come modello unifattoriale)
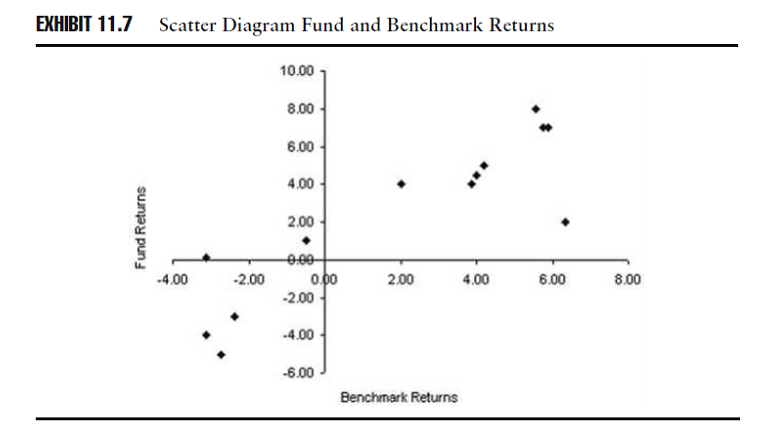
Osservazione 11> È possibile ottenere informazioni sul grado a dispersione tra le due variabili tracciando le due osservazioni. Questo grafico, tracciando la coppia dei rendimenti del fondo e del benchmark periodici, ci permette di visualizzare la relazione tra i rendimenti di fondo e di benchmark. Lo schema 11.7 è un diagramma a dispersione disegnante la relazione tra i rendimenti del fondo (asse y, verticale) e del benchmark (asse x, orizzontale).
Fonte: Investment Performance Measurement (Bruce J. Feibel)
Osservazione 11> Ogni punto rappresenta un rendimento mensile (sia del fondo che del benchmark). La sua distanza dall’asse verticale, o asse delle Y, misurata lungo la scala orizzontale, rappresenta il rendimento del benchmark (rappresentanto sull’asse x, o orizzontale). La distanza del punto dall’asse orizzontale, o asse delle x, misurata sull’asse verticale dal centro, rappresenta il rendimento di fondo (illustrato lungo l’asse y, o verticale). La disposizione dei rendimenti tracciati sul grafico mostra che esiste una forte correlazione tra le due serie di rendimenti. Molte serie di rendimenti sono posizionati in alto a destra o in basso a sinistra dei quadranti del grafico (quandrante 2 e 4 rispettivamente): questa dispersione si verifica perché quando si hanno alti rendimenti di benchmark, si hanno anche alti rendimenti di fondo; vale il caso inverso. Il grafico a dispersione è un indicatore visuale dell’alto grado di correlazione tra il rendimento di fondo e del benchmark; se i rendimenti fossero meno correlati, il grafico a dispersione mostrerebbe più rendimenti negli altri due quadranti.
Ipotizzando che il fondo sia compreso in azioni selezionate da un universo evidenziato rappresentato dal benchmark, ci si aspetterebbe un alto grado di correlazione tra i rendimenti del fondo e del benchmark: per identificare il grado attraverso il quale i rendimenti di fondo variano, data la variabilità nei rendimenti di benchmark, è possibile calcolare una statistica chiamata Beta (vedi, per maggiori informazioni: Capital Asset Pricing Model: il primo modello di mercato per il calcolo dell’adeguata remunerazione del rischio ed il pricing di titoli azionari).
Osservazione 12> Il Beta isola il grado di rischio del benchmark, o anche detto rischio relativo di mercato connaturato nel fondo, in cui il rischio viene definito come la totale variabilità nei rendimenti. Un fondo con un Beta più alto di altri indica che è stato considerato più rischio relativo al benchmark rispetto agli altri. È possibile calcolare il Beta attraverso l’analisi di regressione (built in function di excel o calcolo passo per passo).
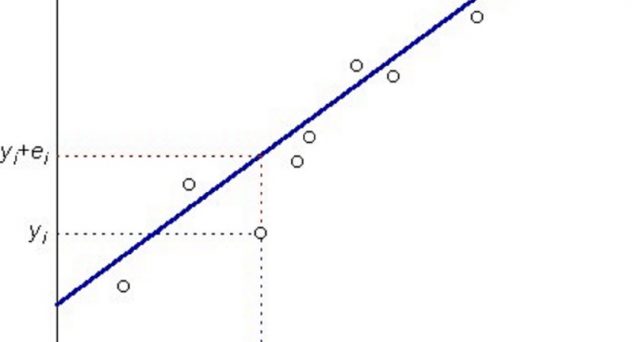
Se i rendimenti fossero fortemente correlati, potremmo immaginare una chiara linea in cui si raggruppano i rendimenti del fondo e del benchmark. Ciò implica la seguente osservazione =>
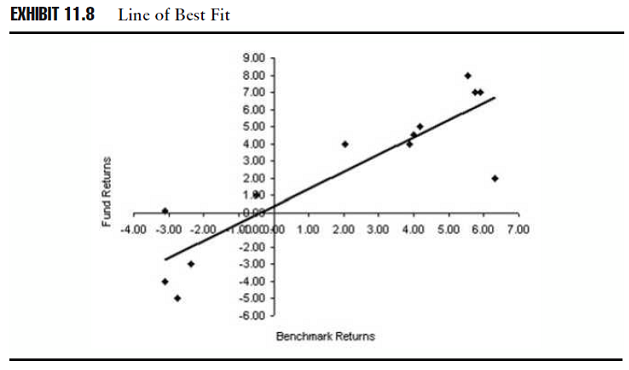
Osservazione 13> Possiamo disegnare una retta, nella parte superiore della linea inclinata verso l’alto nel grafico, dal quadrante in basso a sinistra fino a quello in alto a destra che rappresenta sempre più la tendenza dei dati effettivi. Questa linea best fit rappresenta una relazione lineare tra la coppia di rendimenti. Lo schema 11.8 illustra la linea best fit legata ai rendimenti di fondo e di benchmark.
Fonte: Investment Performance Measurement (Bruce J. Feibel)
È possibile usare la linea best fit per interpolare il rendimento del fondo se ci venisse dato il rendimento di benchmark. Per esempio, noi non abbiamo un’osservazione del rendimento di benchmark uguale all’1% circa, ma possiamo estrapolarla usando la linea best fit e ipotizzare che il fondo di rendimenti del periodo sia leggermente più alto dell’1%. Vediamolo nello schema 11.9.
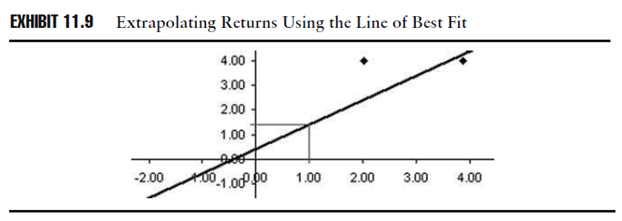
Fonte: Investment Performance Measurement (Bruce J. Feibel)
Questa, di certo, è solo un’ipotesi, ma possiamo evidenziare dalle differenze tra i punti sulla linea e le osservazioni effettive che la stessa linea è la migliore linea per mettere in relazione i rendimenti di fondo e di benchmark. Comunque, non può essere utilizzata per “predire” perfettamente i fondi di rendimento (ci sono altri tipi di rischio da includere per calcolare nel modo più corretto possibile il rendimento di un fondo: vedi l’Arbitrage Pricing Theory ed i modelli multifattoriali). La linea invece è utile come descrizione della relazione. È possibile quantificare la relazione implicata dalla linea best fit usando matematicamente l’equazione di regressione lineare:
Rendimento atteso del fondo = Alfa + (Beta x rendimento di benchamrk)
La retta (equazione) di regressione lineare ipotizza che il valore di una delle variabili sia quantomeno dipendente dall’altra. Sappiamo che un particolare fondo di rendimento è probabilmente più influenzato dai rendimenti di mercato rappresentati dal benchmark piuttosto che dalla relazione opposta, quindi, per calcolare una regressione del fondo contro i rendimenti di mercato, rendiamo i rendimenti del fondo la variabile dipendente e il rendimento di mercato la variabile indipendente. Il rendimento di mercato viene considerato come una variabile casuale mentre il rendimento di fondo diventa parzialmente dipendente.
Osservazione 14> Esistono due coefficienti nell’equazione di regressione:
- Il coefficiente Alfa dell’equazione di regressione rappresenta il valore della variabile dipendente quando la variabile indipendente è uguale a 0 (intercetta della retta di regressione). Possiamo vedere nello schema 11.9 che la linea passa attraverso l’asse del fondo di rendimento nel punto tra lo 0% e l’1%. Quindi Alfa è qualcosa tra lo 0% e l’1%.
- Il secondo coefficiente, Beta, scala il valore del benchmark su e giù per ricavare il valore del fondo di rendimento quando aggiunto ad Alfa. Beta rappresenta l’inclinazione (pendenza) della retta di regressione. Se Beta è uguale a 1, allora l’inclinazione della linea è all’angolo di 45°. Nel nostro esempio, ogni punto percentuale del rendimento sull’asse delle X è associato con la stessa percentuale di rendimento sull’asse delle Y (dopo si aggiunge Alfa).
Osservazione 15> Il valore migliore di Alfa e di Beta sono quelli che minimizzano la distanza tra i valori osservati effettivi e quelli ricavati usando l’equazione.
Questa procedura significa disegnare una linea che minimizza la somma delle distanze individuali dalla linea alle osservazioni individuali. Visto che la linea rappresenta i valori previsti di Y per ogni valore effettivo di X, cerchiamo di minimizzare la differenza elevata al quadrato tra i valori derivati di Y e i valori effettivi di X.
Osservazione 16>Questo processo si chiama regressione dei minimi quadrati ordinari e i valori dei coefficienti che minimizzano le differenze sono calcolati usando formule relative a quelle della varianza e della covarianza.
Regressione Beta
Osservazione 17> Per definire la linea di regressione, si calcola prima il valore della pendenza, o Beta, che può esser espressa matematimaticamente come rapporto fra covarianza fra i rendimenti del fondo e del benchmark e la varianza del mercato benchmark (ulteriormente semplificato nel prodotto fra correlazione fra i rendimenti del fondo e del benchmark ed il rapporto fra le relative deviazioni standard):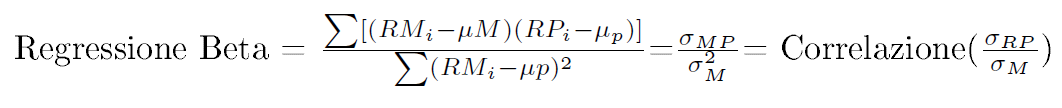
Il foglio excel mostra il calcolo di Beta nel nostro fondo di riferimento, in cui la misura è uguale approssimativamente a 1, indicando che il fondo varia lungo il benchmark. Beta misura quindi come e quanto un’azione fluttua lungo il mercato stesso. Le formule sono differenti dalla covarianza e varianza solo nel caso in cui si eliminasse la quantità dei rendimenti da ogni formula. (Si fa questo perché esse si neutralizzano a vicenda).
Osservazione 18> Beta rappresenta la proporzione della covarianza nei rendimenti di fondo e di benchmark ed è relazionato alla varianza nei rendimenti dei benchmark. Si possono trarre molte conclusioni riguardo i valori di Beta basato su questa formula:
- Se i rendimenti del fondo variassero esattamente in proporzione ai rendimenti del benchmark, questo sarebbe equivalente a sostituire le deviazioni di fondo a numeratore (a destra dell’espressione) con le deviazioni di benchmark. Beta sarebbe uguale a 1 se i rendimenti di fondo variassero nel rendimento medio nella stessa direzione e grado con cui i rendimenti di benchmark variassero nel rendimento medio del benchmark (+1% del fondo +1% del benchmark, -1% del fodno -1% del benchmark).
- Se Beta fosse meno di 1, allora il numeratore sarebbe più piccolo del denominatore. Ciò indica che i rendimenti del fondo sarebbero meno variabili rispetto ai rendimenti di benchmark lungo il periodo, in relazione alle loro medie (titolo difensivo).
- Se Beta fosse maggiore di 1, il numeratore sarebbe maggiore del denominatore, quindi i rendimenti di fondo varierebbero con grado maggiore in rapporto ala media del periodo, rispetto ai rendimenti di benchmark (titolo aggressivo)
- La covarianza vicina allo 0 indica che sono presenti piccole relazioni tra i rendimenti di fondo e di benchmark nel corso del tempo. Ciò comporterà che il numeratore del calcolo di Beta sarà vicino allo 0, che diviso per la varianza negli indici di rendimento, produrrà un risultato vicino allo 0. Quindi un Beta prossimo allo 0 indica che ci sono piccole relazioni tra i rendimenti di fondo e di benchmark.
- Se la covarianza fosse negativa, Beta sarà negativo perché non è possibile avere una varianza negativa. Quindi un Beta negativo indica che c’è una relazione inversa tra i rendimenti di fondo e di benchmark lungo il periodo (titolo superdifensivo)
Lo schema 11.10 sintetizza la spiegazione di Beta.

Fonte: Investment Performance Measurement (Bruce J. Feibel)
Regressione alfa
Osservazione 19> Alfa è uguale all’intercetta dell’asse Y, o il valore del rendimento del fondo quando il rendimento di benchmark è uguale a 0 come dimostrato dall’equazione della regressione. Alfa viene calcolato usando la media dei rendimenti di fondo e di benchmark rettificati da Beta:
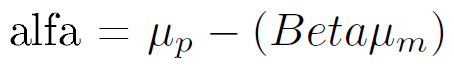
Alfa è uguale alla media dei rendimenti di fondo (portafoglio p) meno Beta che moltiplica la media dei rendimenti del mercato/benchmark. Il foglio excel illustra il calcolo dei coefficienti di regressione utilizzando i dati del nostro fondo di riferimento: il Beta del fondo è approssimativamente uguale a 1, mentre Alfa è approssimativamente uguale a 0.37.
I coefficienti Alfa e Beta producono un’equazione di regressione lineare che descrive la linea di best fit. L’equazione è una descrizione statistica delle serie di rendimenti di fondo e di benchmark storico effettivo. L’equazione suggerisce che i rendimenti di fondo sono uguali al rendimento di benchmark moltiplicato per 1 (Beta) più 0.37% (Alfa).
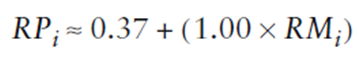
Osservazione 20> Alfa uguale a 0.37% indica che è possibile aggiungere lo 0,37% ad ogni rendimento di benchmark, rettificato da Beta, per eguagliare il rendimento di fondo: ritorneremo sul concetto di Alfa quando parleremo di rendimenti rettificati per il rischio.
Osservazione 21 > Beta uguale a 1 indica che il grado di covarianza nei rendimenti di fondo e di benchmark per eguagliare alla quantità di varianza nei rendimenti dle. È da notare che anche se Beta corrisponde a 1, il rendimento di fondo e di benchmark sono diversi a seconda del periodo individuale. Beta indica che il grado secondo cui la variabilità in un rendimento di fondo è in relazione con la variabilità dei rendimenti di benchmark.
Beta uguale a 1 indica che il grado di rischio relativo al benchmark manifestato dal nostro fondo (covarianza) è uguale a quello del benchmark (varianza). Anche se i rendimenti del fondo variano con lo stesso grado dei rendimenti di benchmark, i rendimenti di fondo sono diversi da quelli di benchmark e noi siamo interessati alla proporzione dei rendimenti di fondo che sono spiegati dal rendimento del benchmark. Determineremo questa proporzione calcolando il coefficiente di determinazione, o R al quadrato, tra i rendimenti di fondo e di benchmark.
Grado di adattamento (di fit)
Osservazione 22> I coefficienti di regressione Alfa e Beta vengono chiamati in causa per costruire una formula lineare che minimizzi le differenze tra i rendimenti del fondo, calcolati usando l’equazione di regressione, e i rendimenti del fondo effettivi. Se tutti i punti dei dati osservati giacessero sulla linea best fit, allora la formula potrebbe essere usata per calcolare precisamente i rendimenti di fondo, dati i rendimenti di benchmark, e i coefficienti Alfa e Beta avranno un alto grado di credibilità.
In quanto i rendimenti osservati non si trovano tutti sulla linea best fit, siamo interessati al grado di errore presente nei coefficienti di regressione. Il grado di errore dipende dal grado di dispersione attorno alla linea di regressione. Maggiore la coppia di rendimenti è dispersa, peggiore sarà la performance della formula di regressione di descrivere la relazione tra i rendimenti.
Osservazione 23> Il coefficiente di determinazione, o R al quadrato, può essere utilizzato per valutare il significato dei coefficienti di regressione. R al quadrato del nostro fondo di riferimento, calcolato nel foglio Excel è 78%. Questo indica che il 78% dei cambiamenti nei rendimenti di fondo possono essere relazionati ai cambiamenti nei rendimenti di benchmark. Questo è un R al quadrato moderatamente alto e merita un alto grado di confidenza nelle statistiche Alfa e Beta rispetto a quando R al quadrato fosse minore. Esso non indica che il 22% dei rendimenti di fondo non sono spiegati dalla variazione nei rendimenti di benchmark. Questa variabilità è invece specificata dal fondo.
Tracking Risk
Osservazione 24> Anche se Beta è circa pari ad 1 i rendimenti del fondo e del benchmark sono differenti per ogni periodo individuale. Il Tracking Tisk quantifica la portata della differenza dei fondi specifici tra i rendimenti del fondo e del benchmark se ipotizziamo che il benchmark sia significativo per il portafoglio; in altre parole il Tracking Risk è più utile se Beta del portafoglio è vicina a 1, altrimenti le statistiche di rilevazione del rischio non avrebbero senso.
Molte strategie di investimento sono pensate per minimizzare le differenze di rendimento fra il benchmark ed il mercato. Un fondo o una strategia che rileva perfettamente il suo benchmark avrà una correlazione uguale a 1. Questo fondo avrà una rilevazione del rischio 0. Il Traking risk ha radici proprio nella gestione dei fondi. La minimizzazione della tracking risk atteso ad un costo accettabile è il fattore chiave nella gestione degli indici dei fondi indice. Altre strategie sono gestite da particolari obiettivi di tracking risk atteso.
Ma la stima del tracking risk atteso è anche una considerazione chiave nella costruzione di molti tipi di portafogli. Alcune modalità di investimento includono particolari limiti fissi intorno alla disposizione di azioni di particolari asset class o segmenti di portafoglio allo scopo di minimizzare il tracking risk atteso rispetto ai benchmark. Il rischio di pianificazione degli stanziamenti e altre tecniche di gestione del portafoglio servono anche per minimizzare il tracking risk.
Questi sono strumenti di stima del tracking risk futuro, per esempio, modelli di rischio multi fattoriali. Qui vedremo la misurazione del tracking risk storico, che fornisce informazioni sia sul successo del manager nel soddisfare i target ditracking risk sia il rischio relativo al benchmark considerato dal manager.
Osservazione 25> Il tracking risk di un fondo o di una strategia corrisponde alla deviazione standard della differenza tra i rendimenti periodici del fondo e del benchmark:
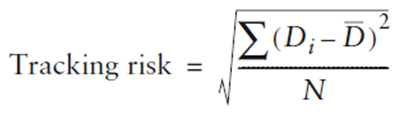
dove: Di = differenze tra i rendimenti peridici del fondo e del benchmark; D soprasegnato = media delle differenze nei r rendimenti suddetti.
Modus operandi
- calcolare le differenze periodiche tra i rendimenti del fondo e del benchmark.
- calcolare la deviazione standard di queste differenze.
Ciò produrrà una statistica del tracking risk con la stessa periodicità dei rendimenti evidenziati, ed è utile perché è espressa in unità di rendimento. Il foglio Excel illustra il calcolo della rilevazione del rischio, 1,95% al mese per il nostro fondo di riferimento.
Osservazione 25> Il tracking risk è una funzione della deviazione standard dei rendimenti di fondo e la correlazione dei rendimenti di fondo e di benchmark. Infatti, è possibile anche calcolare la rilevazione dell’errore con il seguente calcolo:
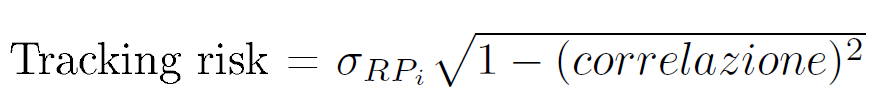
Osservazione 26> Si può annualizzare moltiplicandola per la radice quadrata del numero delle osservazioni dei rendimenti periodici nell’anno:
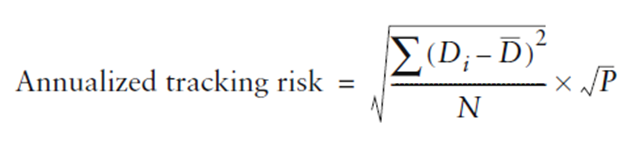
dove P = frequenza delle osservazioni di rendimento (se rendimenti mensili P=12, se giornalieri P = 250 ecc).
Il foglio Excel illustra il calcolo della rilevazione del rischio annualizzato del nostro fondo di riferimento, pari al 6.76%.
Osservazione 27 > I fondi passivi hanno un basso tracking risk perché l’obiettivo è replicare il bechmark (vedi lo SPY su S&P 500 o il DIA su DIJA). Per una strategia gestita attivamente, il tracking fornisce una misura di “rischio attivo” piuttosto che totale. Quando il fondo e il benchmark sono ugualmente rischiosi e i rendimenti sono altamente correlati, ciò implica una bassa rilevazione del rischio. È possibile per un fondo e un benchmark avere rendimenti medi e deviazioni standard simili, ma correlazioni imperfette dei rendimenti. La statistica del tracking risk può identificare questa situazione. Più bassa è la questa metrica, più vicino sarà il rendimento del benchmark. Un problema con la rilevazione di tal misura è lo stesso problema dalla deviazione standard: essa non fornisce informazioni riguardo alla direzione della deviazione; un manager che supera regolarmente il benchmark potrebbe esibire lo stesso tracking risk del manager guidato dal suo benchmark.
Osservazione 28> Uno dei problemi nell’utilizzo della rilevazione del rischio come misura del rischio relativo al benchmark è che è basato sulla deviazione standard, quindi dà lo stesso peso alle deviazioni in rialzo che alle deviazioni in ribasso. Se le deviazioni di benchmark sono normalmente distribuite, questo non è problema.
Osservazione 29> Se il manager può produrre rendimenti con maggior rischio al rialzo rispetto a quello al ribasso, la rilevazione del rischio non coglierà questo fatto: possiamo misurarlo invece calcolando il tracking risk a ribasso, la quale è una deviazione standard dei rendimenti al di sotto di una differenza di target. Per esempio, possiamo calcolare una rilevazione di rischio al ribasso con un target di valore aggiunto uguale a 0. Esistono molte altre versioni possibili dei calcoli.
È possibile anche calcolare come la il traking risk relativo, calcolato come deviazione standard dei rapporti fra i rendimenti del fondo e dell’indice bencmark, ossia
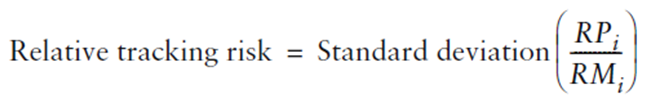
Selezione dei benchmark
Osservazione 30> Il traking risk e le altre statistiche di rischio relativo sono molto sensibili al benchmark selezionato per il confronto: dobbiamo considerare questo quando classifichiamo i portafogli sulla base del relativo benchmark relativo o sulle statistiche di rendimenti aggiustati (o rettificati) per il rischio (cd risk-adjusted return).
Dimostreremo il motivo di ciò nello schema 11.13: abbiamo calcolato Alfa, Beta e R al quadrato dello stesso fondo contro benchmark diversi per dimostrare come i risultati differiscono a seconda del benchmark usato:
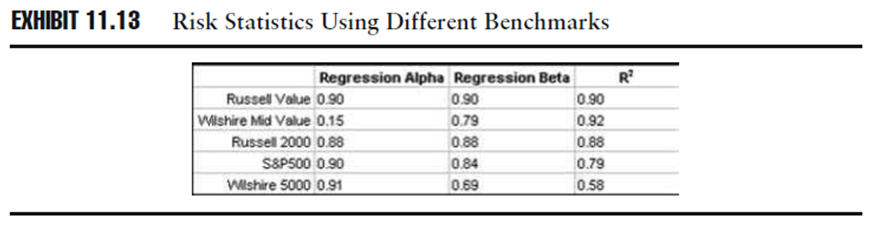
Fonte: Investment Performance Measurement (Bruce J. Feibel)
Le statistiche del rischio relativo, al ribasso e assoluto sono strumenti preziosi per misurare il rischio, ma lasciano ancora senza soluzione alcuni problemi della misurazione della nostra performance. Questi problemi includono quelli riguardanti il fatto che il rendimento maturato sia abbastanza alto da giustificare i rischi quantificati e dato dalla deviazione standard, deviazione al ribasso o tracking risk esibito dalla strategia.
A seguire il file relativo all’esempio di calcolo di quanto sopra esplicato: 5) rischio relativo e capm
Nelle trattazione a seguire verrà affrontato il tema della performance rettificata per il rischio assoluto, o absolute risk-adjusted: Absolute Risk Adjusted Return. Cosa è e come calcolarlo. Scopriamolo!
Come sempre spero di non aver fatto figuracce nei calcoli.
Your best DF.