Il Capital Asset Pricing Model (brevemente CAPM, sviluppato indipendentemente da: Sharpe, 1964; Lintner, 1965; Mossin, 1966) rappresenta un modello di equilibrio dei mercati finanziari ed è diretta conseguenza dell’analisi rischio-rendimento nel piano varianza media del pionieristico lavoro di Henry Markowitz, considerato il padre della modern portfolio theory. Anche in tal caso, per permettere una “facile” lettura e comprensione di ciò di cui si sta parlando, come nel precedente articolo si cerca di semplificare al massimo (per quanto possibile) gli argomenti trattati.
Ipotesi del modello: mercato perfetto dei capitali
- Mercato monoperiodale> la struttura temporale è ancora quella tipica del modello uni periodale, caratterizzato solo dalla data corrente t e dalla data futura s; in definitiva l’orizzonte temporale di pianificazione è lo stesso per tutti gli agenti di mercato
- Assenza di costi di transazione e di gravami fiscali> non ci sono costi di transazione che gravano sugli scambi (commissioni, spread bid-ask, slippage) né gravami fiscali (ad es imposte sui guadagni in conto capitale ecc); sono inoltre sono trascurabili i costi di fallimento
- Titoli infinitamente divisibili> possibile scambiare qualsiasi quantità, anche frazionaria ed infinitesimale, di ciascun titolo
- Possibilità di Short Selling> sono consentite vendite allo scoperto, ossia operazioni finanziarie che consistono nella vendita di titoli non direttamente posseduti dal venditore
- Tasso risk-free i> E’ possibile dare e prendere in prestito, sull’orizzonte temporale da t a s , somme di
danaro di qualsiasi ammontare, al tasso d’interesse non-rischioso i - Agenti avversi al rischio, massimizzatori di profitto (ipotesi di razionalità) e price taker> la funzione d’utilità è crescente e concava; inoltre gli operatori non possono influenzare il meccanismo di formazione dei prezzi tramite azione individuale
- Equilibrio fra domanda e offerta> i prezzi si formano come risultato dell’equilibrio tra l’interazione della domanda e dell’offerta
- Media e covarianza sono le uniche caratteristiche rilevanti per il decisore> Ogni investitore sceglie il proprio portafoglio massimizzando l’utilità attesa. L’utilità attesa è diversa per ogni investitore, ma in ogni caso dipende solo da media e varianza. Ciò equivale ad assumere, come detto prima, che i rendimenti dei titoli seguano una distribuzione normale o che la funzione di utilità sia quadratica (vedi precedente articolo). In conclusione le scelte di portafoglio sono effettuate in base al criterio media-varianza.
- Agenti con aspettative omogenee> Tutti gli investitori dispongono delle stesse informazioni e hanno le stesse aspettative riguardo ai rendimenti futuri dei titoli e alla loro variabilità. Inoltre concordano tutti sui rendimenti attesi dei titoli e sulle loro varianze e covarianze (in altre parole gli investitori dovrebbero avere le stesse aspettative probabilistiche se tendono ad utilizzare informazioni) pubblicamente disponibili
- Tutti gli assets sono trattati sul mercato, anche quelli impropri come il capitale umano
La funzione del CAPM è quella di stimare il rendimento atteso del titolo, o rendimento di equilibrio del mercato, in funzione del rischio sistematico (concetto che fra poco introdurremo), e quindi anche quella di determinare il prezzo di mercato del titolo stesso.
Grazie alle suddette ipotesi (in particolare le ultime 3), sia la frontiera iperbolica che quella frontiera lineare costituiscono un modello di mercato, poiché rappresentano il criterio di ottimalità condiviso da tutti gli agenti.
Capital Market Line
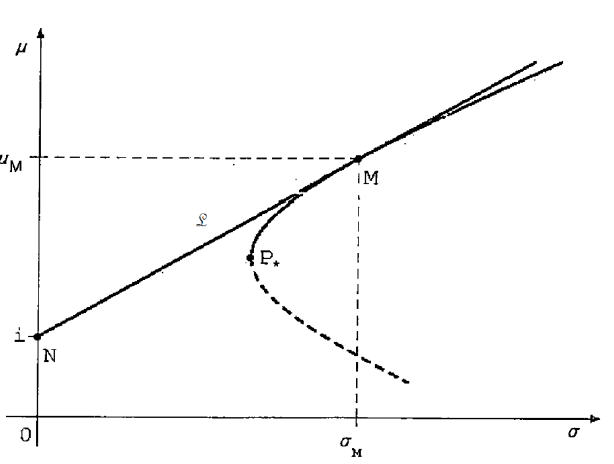
Figura 5: CML
L’equazione della retta è la seguente:
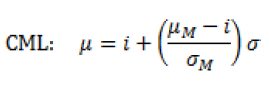
Dove:
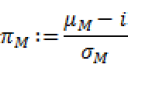
Rappresenta, geometricamente il coefficiente angolare della retta CML, ed economicamente l’indice di Sharpe del portafoglio M (e che ora costituisce il prezzo di mercato per unità di rischio).
La fase di ottimizzazione (ossia l’individuazione della frontiera iperbolica degli N titoli rischiosi con successiva introduzione del titolo risk free per individuare il portafoglio tangente) è ora comune a tutti gli operatori del mercato.
La fase di massimizzazione -dell’utilità attesa- rimane individuale ed ottenuta con il grado soggettivo di avversione al rischio (p es: un operatore che intende sopportare volatilità inferiore a quella del portafoglio di mercato ripartirà il proprio capitale miscelendo il portafoglio M al titolo risk free; un operatore che vuole ottenere rendimenti superiori al portafoglio di mercato assumendosi un maggior grado di volatilità prenderà a prestito denaro al tasso risk free per investire una porzione maggiore del suo capitale disponibile nel portafoglio di mercato)
Il teorema dei due fondi rimane valido ma sarebbe più opportuno chiamarlo teorema del fondo Unico: miscelando il fondo unico (ossia il portafoglio di mercato M) con il titolo risk free, tutti gli individui ottengono un portafoglio ottimale (sulla CML in figura 5, i portafogli a destra di M sono ottenuti prendendo a prestito al tasso risk free per investire il ricavato in una porzione superiore al 100% del capitale disponibile dall’investitore nel portafoglio di mercato; portafogli a sinistra di M sono ottenuti combinando l’investimento privo di rischio ed il portafoglio di mercato).
Prima di passare alla spiegazione della Security Market Line occorre aprire una parentesi sul tema delle aspettative, sulle componenti del rischio, ed il principio del rischio sistematico
Il tema delle aspettative e le componenti del rischio
In condizioni d’incertezza la quotazione di un titolo nell’istante in cui si valuta è nota, ma non è nota la quotazione futura e che invece presenta aleatorietà.
Da ciò deriva che in condizioni di incertezza la formazione dei prezzi può basarsi solamente sull’informazione disponibile nell’istante in cui si valuta: dato che la componente attesa fa parte dell’informazione disponibile agli agenti economici rientra nel meccanismo di formazione del prezzo.
Simmetricamente, non essendo disponibile la componente non attesa nell’istante di valutazione (poiché è una componente aleatoria), questa non dovrebbe essere utilizzata nella formazione del prezzo; c’è però da dire che le valutazioni probabilistiche sulla componente non attesa sono basate sull’informazione corrente, e pertanto rappresenteranno un’altra delle determinanti fondamentali del tasso di rendimento (e di conseguenza del prezzo) e che esprimono l’atteggiamento di fronte al rischio.
Ad esempio, se un operatore utilizza il criterio media – varianza nelle sue valutazioni per determinarne la quotazione di un asset, una sintesi probabilistica della componente non attesa del rendimento può esser fornita dalla varianza.
Si può quindi affermare che le aspettative vengono incorporate nei prezzi correnti. Ciò implica che il realizzarsi di eventi già “previsti” (ossia la parte attesa della notizia) non ha molto effetto sui prezzi poiché non comporta un’alterazione rilevante dell’informazione disponibile. Ciò porta alla seconda affermazione tale per cui le ampie fluttuazioni di prezzo sono determinate da forti alterazioni delle aspettative correnti (cd “effetto sorpresa” di nuove informazioni).
Dato che il tutto è adattato ad un contesto di mercati efficienti occorrerebbe anche definire ciò che viene inteso per efficienza dei mercati ma si sconfinerebbe (i concetti di efficienza allocativa, valutativa, tecnico-operativa e soprattutto informativa sarà oggetto di trattazione futura).
Principio del rischio sistematico
Dato che gli individui sono avversi al rischio la valutazione della componente non anticipata rientra nella formazione del prezzo; ciò perché gli investitori vogliono essere adeguatamente remunerati per investire in una generica attività rischiosa richiedendo, in altri termini, un premio al rischio (extra rendimento).
Dato però che è possibile costruire portafogli diversificati (ossia composti da più titoli) riducendo il rischio (vedi se vuoi, la proprietà di sub additività della volatilità) complessivo, la rischiosità del singolo titolo può essere fortemente ridotta quando il titolo viene inserito in un portafoglio.
Ciò porta quindi ad un altra importantissima considerazione. La componente non attesa dei rendimenti può esser scomposta nella somma di due grandezze:
- il rischio sistematico, ossia che colpisce l’insieme dei titoli trattati e non riguarda lo specifico investimento, e pertanto qualificabile come rischio di mercato
- il rischio specifico (o idiosincratico) che riguarda il singolo titolo, rappresentando quindi una fonte d’incertezza non correlata alle complessive fluttuazioni del mercato
Da tale considerazione deriva il principio del rischio sistematico (o del premio a rischio diversificato): in un mercato efficiente il rendimento atteso di un investimento dipende solo dal suo rischio sistematico poiché quello specifico può esser annullato a costo zero tramite diversificazione.
Vedi, se vuoi, l’esperimento di Fama per vedere come agisce la diversificazione sulla volatilità tramite l’aggiunta progressiva di titoli in portafoglio (Fama rileva che gran parte della diversificazione si realizza già con portafogli equally weighted di 15/20 titoli).
Security Market line
Avendo fatto le considerazioni sul portafoglio di mercato, sulle componenti del rischio ecc. occorre analizzare le relazioni sul singolo titolo.
Nel modello media varianza l’equazione della CML fornisce una relazione tra rischio e rendimento relativa ai soli portafogli efficienti. Tramite delle considerazioni di equilibrio, è possibile estrapolare una relazione tra rischio e rendimento valida per tutti i titoli o portafogli di titoli quotati sul mercato.
Una misura fondamentale ricavata dell’equazione del CAPM (vedi, se vuoi, il teorema di Linearità dei premi al rischio), che stabilisce la proporzionalità fra l’extra rendimento (o premio al rischio) del generico titolo e l’extra rendimento del portafoglio di mercato, è data dal β del titolo, grandezza che rappresenta la sensibilità del generico titolo alle fluttuazioni del portafoglio di mercato.
Il β costituisce il contributo marginale del generico titolo alla rischiosità del portafoglio di mercato e rapportato alla volatilità del portafoglio di mercato stesso, informando sulla variazione % attesa del rendimento in eccesso del titolo in corrispondenza della variazione dell’1% dell’extra rendimento del portafoglio di mercato (se β è uguale a 0,7 ogni variazione dell’1% del rendimento del portafoglio di mercato M determina una variazione media dello 0,7% sul rendimento del titolo).
Il β rappresenta, in altre parole, la misura del rischio sistematico (normalizzata). Da ciò deriva che la volatilità di un titolo preso singolarmente è data dal rischio sistematico e dalla porzione di rischio specifico (vedi il suddetto principio del rischio sistematico)
Partendo dall’equazione del CAPM ed effettuando alcuni passaggi algebrici si arriva alla seguente relazione, chiamata Security Market Line (SML)
μk = i + βk ( μM – i )
Dove: μk è il rendimento atteso del generico titolo k (o portafoglio k), βk è la sensibilità del generico titolo k alle fluttuazioni del mercato, μM è il rendimento atteso del portafoglio di mercato ed i è il tasso di rendimento del titolo privo di rischio.
Dal punto di vista grafico
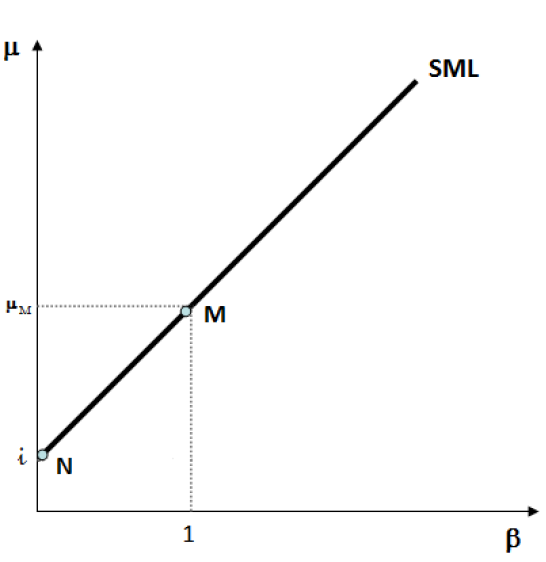
Figura 6: SML
La suddetta relazione, a differenza della CML, è valida in condizioni di equilibrio per tutti i titoli (o portafogli di titoli), efficienti o no.
Essendo definita come il luogo dei punti corrispondenti ai titoli (o portafogli di titoli) in equilibrio, ogni scostamento dalla SML causa disequilibri e, in particolare, possibilità di arbitraggi privi di rischio: asset al di sopra della SML sono considerati sottovalutati perché per un dato ammontare di rischio (beta), producono un rendimento più elevato di quanto atteso dalla SML; simmetricamente gli asset posizionati sotto la linea sono sopravvalutati perché, per un determinato ammontare di rischio, producono un rendimento inferiore di quanto atteso dalla SML. Inoltre la SML è definita anche per valori negativi di beta, poiché è possibile trovare titoli o portafogli negativamente correlati con il portafoglio di mercato.
Quanto detto porta ad effettuare delle considerazioni
- il portafoglio di mercato, banalmente, ha β = 1
- se β = 0 si ha a che fare con un’attività non correlata col mercato e potrebbe o avere solo rischio specifico o essere un un titolo teoricamente privo di rischio
- se β > 1 il titolo è detto aggressivo poiché dovrebbe mediamente offrire rendimenti superiori al mercato
- se 0 < β < 1 il titolo è detto difensivo poiché offre rendimenti inferiori al mercato
- se β < 0 il titolo è detto super difensivo poiché è negativamente correlato col mercato, producendo in media performance positive quando il mercato scende e performance negative quando il mercato sale (un investitore razionale potrà inserire anche questi titoli in portafoglio poiché, nonostante siano sub ottimali producendo un rendimento atteso inferiore a quello privo di rischio, forniscono una sorta di assicurazione contro la recessione, rappresentando parte di un portafoglio ben diversificato.)
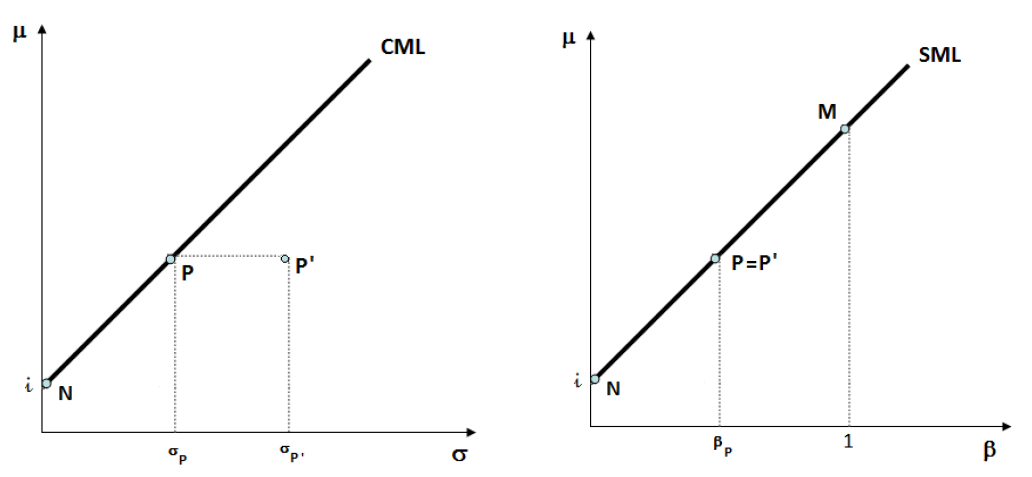
Figura 7: CML vs SML
Dati due portafogli, P e P’, il primo ha solo rischio sistematico mentre il secondo è caratterizzato anche da rischio specifico nel senso che σp<σp’. Sulla SML P e P’ sono considerati uguali, in termini di rischiosità, poiché secondo il CAPM la remunerazione di un’investimento è solo funzione del rischio sistematico.
Applicazione del CAPM e verifica empirica
CAPM come modello di valutazione di un titolo: determinazione del prezzo e di eventuali sopra/sotto valutazioni
Determinando il rendimento atteso di un titolo in funzione del suo rischio sistematico (ossia comune al mercato), una volta stimati i flussi di cassa futuri, è possibile attualizzarli al tasso di rendimento determinato con il CAPM per determinare il fair value di un titolo: in tal modo si stabilisce un criterio per stabilire ad esempio se il prezzo di mercato di un titolo sia sopra o sottovalutato rispetto al suo valore intrinseco). In altre parole, teoricamente un’attività finanziaria è correttamente prezzata se il prezzo osservato sul mercato è uguale a quello determinato tramite il CAPM. Se il prezzo di mercato è più alto (più basso), l’attività è sovrapprezzata (sottoprezzata).
Se supponiamo che ia sia il tasso di rendimento determinato dal CAPM per il titolo a, Vt il generico flusso di cassa generato in una generica data t, allora Va è il fair value (“il prezzo corretto”, o valore intrinseco) del titolo A determinato come somma dei flussi di cassa futuri attualizzati (ossia espressi in valore attuale). Questa equazione è una forzatura se applicata ad un modello di valutazione di un titolo azionario (si pensi solo al fatto che un azione ha “durata indefinita” rispetto ad un obbligazione) ma rende l’idea (per i vari modelli si possono prendere ad esempio il dividend discount model o il total payout model ed il modello dei flussi di cassa scontati)
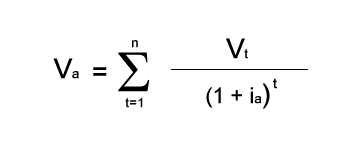
Alternativamente, dato un qualunque modello di valutazione, è possibile risolvere l’equazione per la valutazione di un’attività finanziaria in funzione del tasso di attualizzazione, supponendo di osservare un’attività correttamente prezzata sul mercato. In pratica si pone Va uguale al prezzo di mercato osservato e Ia come incognita dell’equazione risolta tramite procedure numeriche: se il tasso di sconto risultante è minore (maggiore) di quello implicato dal CAPM, l’attività finanziaria è sovrapprezzata (sottoprezzata).
Impossibilità d’investimento al tasso non rischioso: Zero-Beta CAPM
Problema: se non esiste un titolo privo di rischio si può ancora utilizzare il CAPM?
Soluzione: Black (1972) ha proposto di ottenere una relazione lineare fra rischio e rendimento per il generico titolo k sostituendo il titolo non rischioso con il titolo (o portafoglio di titoli) z a βz=0.
Di conseguenza la CML assume la seguente forma:
μk = μz + βk ( μM – μz )
E la frontiera efficiente nel piano deviazione standard-rendimento medio (o atteso) è la seguente
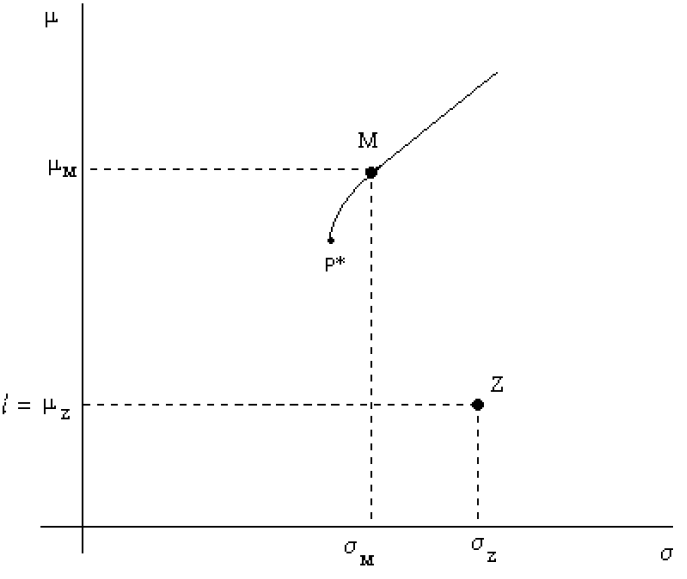
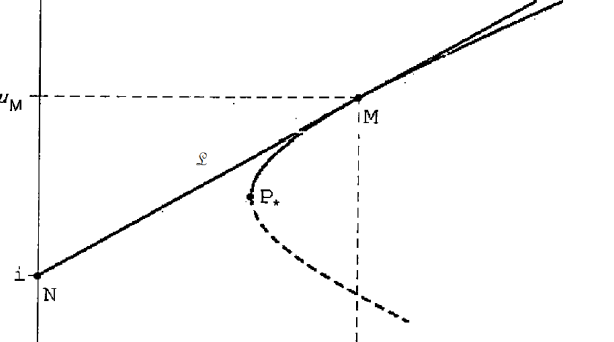
Figura 8: Zero-Beta CML
Dato che la correlazione fra il titolo a beta uguale a 0 ed il mercato è nulla il titolo z non può essere efficiente: giace al di sotto del punto P* del portafoglio a varianza minima ed il suo rendimento atteso è minore di quello di P*.
La frontiera efficiente (lineare) si ottiene ora miscelando il portafoglio z con il portafoglio di mercato M, essendo rappresentata da una retta con intercetta pari a μz e tangente al portafoglio M.
Per utilizzare il modello è necessario che siano consentite vendite allo scoperto poiché, dato che sul mercato prevale la presenza di titoli a correlazione positiva, la formazione di un portafoglio a Beta 0 si ottiene detenendo titoli con quote “negative”.
Verifica empirica
Una volta creato è stata sentita subito l’esigenza di testare la validità empirica del CAPM, dando avvio ad un enorme quantità di ricerche con risultati molte volte contrastanti.
Il punto cruciale è che il CAPM stabilisce una relazione fra aspettative su variabili aleatorie. Il problema diventa quindi testare un’ipotesi sulle aspettative di variabili aleatorie guardando alle realizzazioni osservate di queste variabili aleatorie.
Per effettuare delle verifiche empiriche è allora possibile scrivere l’equazione CAPM in forma ex-post (verificare se, in media, il rendimento realizzato è uguale a quello atteso):
Ip(Θ) = i + α0 + α1 βp + εp(Θ)
Dove p si ipotizza essere un portafoglio opportunamente costruito per abbassare gli errori nella stima del β. Se il CAPM è corretto, testando il modello a fronte del rendimento Im(Θ) verificatosi nel mercato si dovrebbero ottenere i seguenti risultati:
- L’intercetta α0 non dovrebbe essere significativamente (ossia statisticamente) diversa da 0
- βp dovrebbe essere l’unico fattore che determina variazioni nei rendimenti; in altre parole il rendimento I dipende solo dal β, che cattura correttamente tutto il rischio presente nei mercati
- il modello rappresenta il “best fit”, ossia che approssima meglio i dati
- il coefficiente α1 dovrebbe essere circa uguale all’extra rendimento di mercato Im(Θ) – i
- nel lungo periodo il rendimento Im(Θ) realizzato dal mercato è maggiore del tasso risk free i
Numerose ricerche empiriche hanno dimostrato la non validità del CAPM, osservando in particolare che:
- solo i punti 3 e 5 risultano soddisfatti
- l’intercetta α0 è significativamente diversa da 0
- α1 è minore dell’extra rendimento del mercato
- βp non cattura correttamente tutto il rischio presente nel mercato, rappresentando una misura distorta del rischio sistematico
La maggiore critica al CAPM è stata mossa da Roll (1977), e basata sul fatto che il portafoglio di mercato non è realmente osservabile, e che i portafogli utilizzati come proxy (es SP500) del portafoglio di mercato non sono validi. Il portafoglio di mercato dovrebbe infatti contenere tutte le attività, anche quelle non quotate o improprie come il capitale umano.
Queste osservazioni hanno indotto ad utilizzare la suddetta equazione, nota come Empirical Market Line
Ip = i + α0 + βp (Im -i)
Considerazione importante: l’intercetta α0, nota alfa di Jensen, se maggiore di 0 misura l’extra rendimento del portafoglio P non giustificato dalla sua rischiosità. Può esser quindi utilizzata come misura di performance storica di un titolo (o portafoglio di titoli) rispetto ai rendimenti attesi dalla SML.