L’obiettivo della trattazione è spiegare nel modo più semplice e comprensibile possibile ciò che ha dato vita ai modelli di asset allocation attuali, senza entrare troppo nel gergo tecnico del “matematichese” (per quanto si voglia, a volte occorre utilizzarlo) ed invogliare il lettore ad esplorare il mondo della portfolio selection. Si faranno pertanto delle forzature e si ometterà di fare delle considerazioni, a volte, per rendere bene il concetto di ciò che si vuole esprimere.
Il lavoro pionieristico di Markovitz: la frontiera delle opportunità, il portafoglio a varianza minima e la frontiera efficiente
I lavori pionieristici di Markowitz (1952, 1959) segnano l’inizio della Modern Portfolio Theory (MPT).
I modelli di selezione di portafoglio hanno pertanto lo scopo di determinare una composizione dello stesso, in termini di frazioni percentuali di capitale investito in ogni titolo, tale da soddisfare delle caratteristiche di “ottimalità” su parametri quali guadagno (inteso ad esempio come il rendimento medio, o anche detto atteso atteso) e rischio (inteso ad esempio come misura di dispersione del rendimento dalla media, la più popolare è la deviazione standard): viene considerato ottimale (o efficiente) un portafoglio che presenta il massimo rendimento per un dato livello di rischio o, specularmente, che presenta minimo rischio per un dato livello di rendimento.
L’idea di partenza di Markowitz era quella di risolvere un problema di ottimizzazione multi obiettivo, al fine di calcolare punti pareto-ottimali su un piano a due dimensioni, in cui sull’asse delle ascisse figura la varianza, mentre sulle ordinate la media (si ricorda che la deviazione standard è la radice quadrata della varianza, e che rende la varianza “confrontabile” al dato su cui si calcola, ossia il rendimento medio: se il rendimento medio è espresso in % la deviazione standard è espressa %): nel caso di due obiettivi, un punto è detto pareto ottimale se e solo se non è possibile migliorare il valore di un obiettivo senza penalizzare l’altro (in altre parole non esiste un altro punto che assicura un valore più elevato per entrambe le funzioni).
L’insieme di tali punti forma la frontiera efficiente dei titoli rischiosi, calcolata, come detto prima, risolvendo un problema di ottimizzazione multi obiettivo in cui occorre massimizzare il rendimento atteso (media) e minimizzare la varianza: queste due metriche sono identificate rispettivamente come misure di guadagno e di rischio (obiettivi peraltro in contrasto tra loro, e da cui nasce il cd trade-off rischio/rendimento). Il problema è stato poi riformulato in modo più semplice, considerando un solo obiettivo ed inserendo l’altro fra i vincoli del problema di ottimizzazione vincolata: ad esempio minimizzare la varianza ed imporre un vincolo di rendimento minimo da cui partire per costruire il set di portafoglio efficienti.
Si parte dalla definizione di un obiettivo globale, ossia massimizzare l’utilità attesa (la teoria dell’utilità attesa, che guida i processi di decisione in condizione di incertezza, sarà oggetto di approfondimento in un prossimo articolo), per scomporlo in obiettivi parziali: minimizzare il rischio e massimizzare il guadagno. Solo dopo aver agito sugli obiettivi parziali può esser garantito l’obiettivo globale
Questo lavoro è stato il punto di partenza per lo sviluppo del primo modello di mercato avente ad oggetto il pricing ed il calcolo dell’adeguata remunerazione del rischio di titoli azionari, il Capital Asset Pricing Model (brevemente CAPM, sviluppato indipendentemente da: Sharpe, 1964; Lintner, 1965; Mossin, 1966)
Costruzione “naive” della frontiera efficiente: dall’insieme delle opportunità alle opportunità di frontiera ed alla frontiera efficiente
Si definiscono (non me ne volete, si usa l’alfabeto greco):
- φ(X) (lettera phi ma maiuscola, ossia quello “strano cerchio con una riga in mezzo”, in figura 1) come la generica misura di rischiosità della variabile casuale X, ossia i rendimenti (tutto si “gioca” in ambito probabilistico ed i rendimenti, così come i prezzi azionari da cui si ricavano, sono considerati variabili casuali)
- E(X) come la speranza matematica, ossia il valore atteso (o valore medio), dei rendimenti
- Chi (la strana X) come l’insieme delle opportunità (area grigia in figura 3), in cui ogni punto rappresenta una possibile combinazione di rischio e guadagno di un determinato titolo azionario
- β come la frontiera delle opportunità
- ε la frontiera efficiente
Nell’insieme Chi sono fondamentali le opportunità di frontiera, ossia quei punti che hanno ha minima rischiosità tra tutte le opportunità caratterizzate dallo stesso valore atteso.
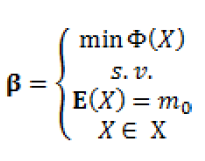
Figura 1: minimizzare la rischiosità (varianza) partendo da un fissato valore di guadagno (rendimento medio)
Che tradotto significa: minimizzare la rischiosità (che viene individuata con la varianza) della variabile casuale X (i rendimenti) per ogni fissato livello di valore atteso di X, con tale variabile appartenente all’insieme delle opportunità Chi.
In pratica, vedendo la figura 3, fissato il livello m0 di rendimento atteso si individua il punto P0 appartenente all’insieme delle opportunità, che rappresenta l’opportunità di frontiera. Al variare di m0 (m1, m2 ecc) nell’insieme Chi si individuano tutte le opportunità di frontiera che costituiscono la frontiera di Chi, altrimenti detta frontiera delle opportunità β (in figura 3 è rappresentata dalla funzione parabolica, formata sia dalla linea tratteggiata che da quella continua ed evidenziata in nero).
Su β possono poi essere individuate altre opportunità che hanno stessa rischiosità ma diverso valore atteso.
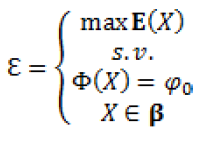
Figura 2: massimizzare il guadagno (rendimento atteso) dato un livello fissato di rischiosità (varianza)
Il luogo delle opportunità efficienti viene quindi chiamato frontiera efficiente (ossia il sottoinsieme ε appartenente a β, rappresentato dalla curva nera che parte dal punto P1, ossia il punto a varianza minima, ed arriva al punto di massimo valore atteso al punto P4)
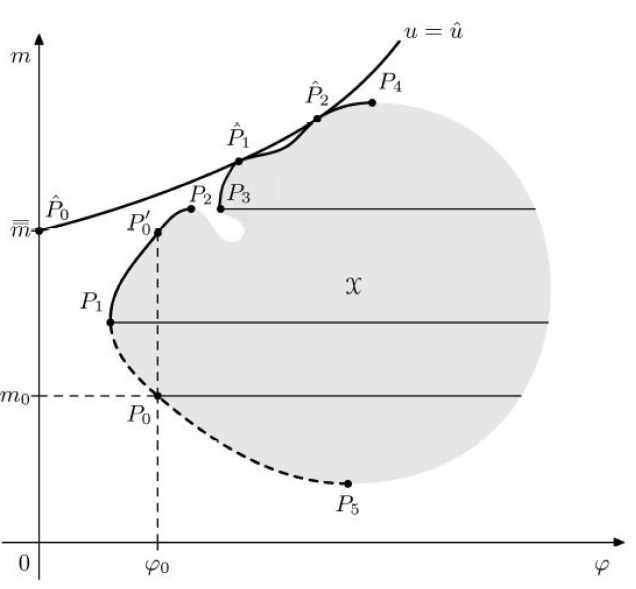
Figura 3: costruzione della frontiera delle opportunità e della frontiera efficiente
I punti della frontiera efficiente costituiscono dei punti di ottimo paretiano o pareto efficienti (il nome deriva dall’economista Vilfredo Pareto): l’individuazione della frontiera efficiente ε assicura quindi che non è possibile spostarsi su di essa per migliorare uno degli obiettivi parziali (ad esempio aumentare il valore atteso) senza penalizzare l’altro (ossia senza aumentare la rischiosità). Sul grafico sopra la frontiera efficiente è rappresentata dalla curva nera che parte dal punto P1 (punto a rischiosità minima) ed arriva al punto di massimo valore atteso (la frontiera delle opportunità β invece continua anche sulla parte tratteggiata)
Individuando la frontiera efficiente il problema di ottimizzazione consistente nell’analizzare gli obiettivi parziali è risolto. Ora il problema decisionale riguarda la scelta, fra i portafogli efficienti, di quello più adatto all’individuo (data la sua avversione al rischio) e che quindi massimizza l’utilità attesa: sulla frontiera efficiente si individua il punto di massimo dell’obiettivo globale, un punto P della frontiera efficiente, tangente (e quindi situato) alla (sulla) curva d’indifferenza con il valore u più elevato dell’utilità attesa.
Si ricorda il lettore che il fine rimane quello di determinare i pesi % (frazioni di capitale investito) dei titoli che compongono i vari portafogli sulla frontiera delle opportunità, tali da rispecchiare determinate caratteristiche
Il tutto, come detto, viene adattato nel modello media-varianza: la media dei rendimenti come metrica di guadagno e la varianza (o la deviazione standard) come metrica di rischiosità (anche se è più corretto considerarla come misura di variabilità e non di rischio, meglio identificata da altre grandezze che saranno oggetto di trattazione futura). Il criterio dell’utilità attesa nella realtà è tuttavia pienamente compatibile col modello media-varianza solamente in due casi:
- Quando l’individuo decisore sceglie una funzione di utilità quadratica (perché non esistono termini di ordine superiore al 2°)
- Quando i rendimenti sono distribuiti secondo una distribuzione normale multivariata (poiché la media e la varianza descrivono correttamente tutta la distribuzione dei rendimenti, rappresentando in modo corretto, la prima il punto centrale della distribuzione e la seconda l’ampiezza; la normale è infatti una distribuzione simmetrica e quindi il momento centrale del 3° ordine, l’asimmetria, è pari a 0; anche la kurtosi non è rilevante in questa distribuzione): nella realtà la distribuzione dei rendimenti può assumere valori negativi ma non sotto 1 (ossia il -100% del capitale investito, mentre la normale assume valori che vanno da +infinito a -infinito), ed è stato spesso provato (vedi ad es.: Lo e MacKinlay, 1999; Cont, 2001; Brooks e Kat, 2002; Ortobelli e altri, 2003) che la distribuzione empirica dei rendimenti presenta caratteristiche diverse dalla normale; potrebbe non essere stazionaria (i relativi parametri, come media e varianza, potrebbero non essere stabili nel tempo), presentare asimmetrie (sovente negative per le azioni) ed avere code più spesse (= eventi estremi più probabili) della normale.
Tuttavia, su un campione di dati elevato l’approssimazione con la distribuzione normale a volte è utilizzabile (vedi la legge dei grandi numeri). Inoltre, esistono delle ricerche che dimostrano che, anche quando i rendimenti non sono distribuiti come una una normale, l’approccio media-varianza fornisce ancora una buona approssimazione del criterio dell’utilità attesa (vedi, fra i vari: Markowitz, 2012b; Carleo e altri, 2016)
La frontiera efficiente ed il teorema dei due fondi
Ipotesi: A e B sono due portafogli della frontiera delle opportunità β
Tesi: la frontiera delle opportunità può essere costruita con una combinazione di questi due portafogli (cioè con due soluzioni del problema di Markowitz)
Implicazione: il teorema afferma che, almeno teoricamente, due portafogli efficienti bastano per costruire ogni alternativa d’investimento ottimale ripartendo il capitale solo fra il fondo A ed il fondo B
Frontiera efficiente lineare
Se ipotizziamo di inserire anche un titolo “convenzionalmente” definito privo di rischio è possibile diminuire la varianza ed espandere l’insieme delle opportunità, conferendo alla frontiera un andamento lineare anziché iperbolico (iperbolico perché in tal caso ci si riferisce alla deviazione standard e non alla varianza): la frontiera ora viene definita linea di efficienza.
In altre parole, considerando un generico titolo non rischioso (che teoricamente implica rendimento certo e varianza nulla) e miscelandolo con un portafoglio di titoli rischiosi sarà sempre possibile ampliare la frontiera delle opportunità fino a includere quella a rischio nullo.
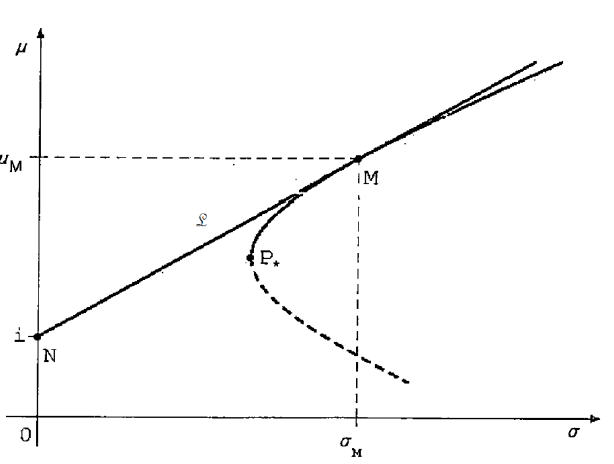
Figura 4: Linea di efficienza
Se indichiamo con i il rendimento del titolo N privo di rischio (p es un titolo di stato AAA), e considerando che un portafoglio rischioso ha praticamente sempre un rendimento atteso superiore a quello risk free (si assume l’ipotesi di avversione al rischio), possiamo definire la misura dell’extra rendimento, ossia il premio al rischio che esprime il compenso, in termini di rendimento atteso, richiesto dall’investitore per assumere un determinato livello di rischio):
δm= μM – i
Dove μM indica il rendimento atteso dal portafoglio M. Se poi indichiamo con σM la volatilità (misurata dalla deviazione standard) del portafoglio M otteniamo la seguente equazione della linea di efficienza:
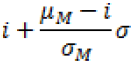
Da un punto di vista geometrico ora, la scelta ottimale si ottiene selezionando come portafoglio rischioso il punto M di tangenza tra la frontiera iperbolica e la semiretta uscente da N (altre linee di efficienza con pendenza inferiore sarebbero infatti sub ottimali: se ad esempio avessimo una linea di efficienza che passasse per il punto a rischiosità minima P* in figura 4, scegliendo un portafoglio con livello di rischiosità σM si otterrebbe un rendimento medio meno elevato di quello del portafoglio M)
Possiamo inoltre fare un’altra considerazione: il rapporto fra l’extra rendimento e la deviazione standard del portafoglio M misura l’extra rendimento per unità di rischio assunto o anche detto costo per unità di rischio
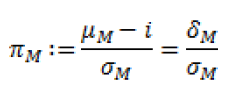
Tale rapporto è noto anche come indice di Sharpe: si può quindi affermare che in un mercato con n+1 titoli (n rischiosi e uno risk free) i portafogli efficienti sono quelli con π uguale a quello del portafoglio M. In altre parole, fra tutte le semirette la linea di efficienza è quella con indice di Sharpe più elevato. Ciò implica che fra i portafoglio che non contengono il titolo N, il portafoglio M è quello con π più elevato: extra rendimenti per unità di rischio così elevati possono essere ottenuti solo miscelando N e M.
Nella pratica, con tale modello, quando si costruiscono portafogli si deve conoscere prima il rendimento atteso e la volatilità di ogni singolo titolo, e poi determinare rendimento atteso e volatilità del portafoglio. Se però gli operatori hanno diverse aspettative otterranno risultati diversi e di conseguenza diversi indici di Sharpe.
Sebbene oggetto di critiche (vedi ad esempio quelle di cui sopra) il modello di Markowitz rappresenta la base da cui partire per capire i modelli di asset allocation più sofisticati (basati ad esempio sulla risk parity o su misure più propriamente definite di rischio rispetto alla varianza, come il VAR, il C-Var e altri lower partial moments), e rientranti comunque nel campo matematico dell’ottimizzazione vincolata.
Il Capital Asset Pricing Model, oggetto di trattazione del prossimo articolo, prende il modello media-varianza riferito al singolo individuo decisore e lo proietta in un modello di mercato “condiviso” da tutti gli operatori.