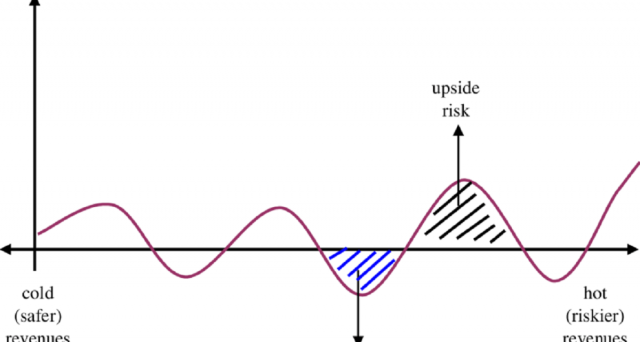
Nel precedente articolo (Vedi: Come analizzare il “rischio assoluto” e la distribuzione dei rendimenti tramite Excel? Scopriamolo!) abbiamo analizzato come misurare il rischio assoluto e descrivere la distribuzione dei rendimenti. In questa sede la trattazione sarà concentrata sul rischio a ribasso (o Downside Risk) dato che la deviazione standard può non andare sempre bene. Niente paura se sarà presentato del “matematichese”, ci sarà in allegato un foglio Excel che ti mostrerà la via (si consiglia di imparare l’utilizzo di Excel)!
Come detto in precedenza la deviazione standard è una buona misura della variabilità in una serie di rendimenti distribuiti normalmente.
Osservazione 1> Mentre la deviazione standard descrive la variabilità in rendimenti sopra e sotto al rendimento medio, noi siamo ontologicamente interessati al rischio inglobato dai rendimenti sotto il rendimento medio. In quanto la distribuzione normale implica un ugual numero di rendimenti sopra e sotto il rendimento medio, la deviazione standard può aiutarci a differenziare il calo del rischio di due strategie di investimento. Un fondo con una deviazione standard del 20% ha maturato meno volatilità sia attraverso guadagni in rialzo sia attraverso cali di perdite rispetto ad un fondo con deviazione standard al 30%.
Osservazione 2> La deviazione standard non è una buona misura della variabilità di rendimento quando la distribuzione dei rendimenti è inclinata, o comunque non normale. Se la distribuzione dei rendimenti fosse distribuita non normalmente, ci aspetteremo di maturare un diverso numero di rendimenti rispetto a quelli “predetti” dalla distribuzione normale in un particolare punto della distribuzione stessa. Per esempio, se avessimo una strategia che facesse utilizzo di opzioni put, non ci dovrebbero essere grandi perdite negative che altrimenti avremmo potuto sperimentare.
Oltre al problema della distribuzione non normale, ci sono molte critiche sulla deviazione standard come surrogato del rischio statistico.In questo parte verranno presentate queste critiche e si esamineranno alcune modifiche al rischio nella struttura delle metriche designate ad affrontare questi difetti.
Difetti della deviazione standard
Se si metto sullo stesso piano la variabilità di rendimenti attorno al rendimento medio, con il ‘rischio’, allora si accetta che la deviazione standard dei rendimenti è una misura accettabile del rischio.
Osservazione 3> Considerare la variabilità di rendimento attorno al rendimento medio non è proprio corretto rispetto a come si concettualizzerebbe il rischio di investimento. Ci sono due ragioni per questo:
- il centro attorno al quale la direzione standard calcolata è il rendimento medio storico;
- il deviazione standard tratta le deviazioni di rendimento positive e negative dalla media con ugual misura (essendo uno scarto quadratico medio).
- le deviazioni di rendimento che comprendono la deviazione standard vengono calcolate usando il rendimento medio come rendimento di riferimento. Il rendimento medio è una metrica della media del rendimento di un rendimento maturato storicamente. Il concetto di deviazione standard tratta come contributi al rischio qualsiasi rendimento che cade in qualunque parte dello stesso rendimento medio. Gli investitori possono comunque avere un punto di vista differente per il concetto di rischio. Ad esempio, investendo in azioni ordinarie di grandi compagnie che abbiano maturato un rendimento medio annuale del 13%, per raggiungere i nostri scopi comunque dovremmo aspettarci di guadagnare un rendimento minimo dell’11% ad anno. In questo caso, considereremo i rendimenti annuali al di sotto del 11% come rischiosi, e non quelli sotto al 13%.
- la deviazione standard considera uguali le deviazioni di rendimento positive e le deviazioni negative. Per molti è contro natura che i rendimenti che sono sopra alla media di rendimento dovrebbero dare un contributo positivo alla misurazione della rischiosità. Per esempio, se la media di rendimento mensile di un investimento fosse l’1% e ci fosse un mese con un rendimento del 10%, dovremmo considerare quanto avvenuto come un evento fortunato piuttosto che un evento rischioso.Ma il rendimento del 10% avrà lo stesso effetto del rendimento a -10% sulla deviazione standard dei rendimenti. La volatilità creata dalle perdite ha più impatto sul nostro su un investimento rispetto alla volatilità creata dai guadagni in eccesso del rendimento medio. Questa seconda critica viene meno quando i rendimenti sono distribuiti normalmente: se la metà dei rendimenti sta sopra il rendimento medio e l’altra metà al di sotto, ogni classificazione dei portafogli basata sul rialzo e ribasso del rischio sarà la stessa. Ma questo non è il caso: i rendimenti non sono distribuiti normalmente o l’investitore ha un obiettivo di rendimento differente dal rendimento medio.
Rischio assoluto (absolute risk) e rischio al ribasso (downside risk) a confronto
Osservazione 4> Per scandagliare tali argomenti gli analisti hanno sviluppato una framework per misurare il rischio al ribasso. Le statistiche del rischio al ribasso considerano come rischiosi solo quei rendimenti che sono al di sotto del rendimento di riferimento specificato.
Preso atto di ciò (lett: data l’illustrazione dei problemi con la deviazione standard, che guida lo sviluppo delle misure del rischio al ribasso), considerate un investitore che definisce un evento come rischioso nel momento in cui i rendimenti di ogni periodo sono negativi. Per questo investitore, il rischio è la perdita possibile di capitale. Lo schema 10.1 mostra due portafogli alternativi per questo investitore. Il fondo 1 ha una deviazione standard di rendimento uguale a 4,13%, mentre quello del fondo 2 è molto più bassa, 0,35%.

Fonte: Investment Performance Measurement (Bruce J. Feibel)
Il fondo 2 ha una deviazione standard più piccola ma i rendimenti sono raggruppati intorno al 10%. A dispetto di ciò, malgrado la deviazione standard sia più piccola, un investimento nel fondo 2 perderebbe ¾ del suo capitale, mentre un investimento nel fondo 1 incrementerebbe, anche se non regolarmente, nel tempo. Questo esempio è un caso estremo in cui le deviazioni standard, non usate in tandem con altre metriche, non si accordano con il nostro senso di rischio.
Osservazione 5> Le misure al ribasso del rischio si focalizzano sui rendimenti che cadono al di sotto di un certo valore. Esse rivolgono le critiche alla deviazione standard in tal modo:
- Il punto di riferimento al di sotto di quello che noi consideriamo un rendimento rischioso viene stabilito secondo la strategia di investimento del fondo (o del singolo investitore) piuttosto che usando il rendimento medio.
- Solo le deviazioni di rendimento al di sotto di questo obiettivo di rendimento vengono pesate nella misura del rischio.
- Le misure a ribasso del rischio rappresentano il rischio meglio della deviazione standard quando la distribuzione dei rendimenti è non-normale.
Semideviazione (Semideviation)
Le statistiche del rischio al ribasso sono basate sul modello della deviazione parziale, o semideviazione.
Osservazione 6> La semideviazione è la deviazione standard dei rendimenti che cadono sotto il rendimento medio. Viene calcolata come la radice quadrata della semivarianza, e la semivarianza sotto media è la varianza dei rendimenti sotto il rendimento medio. La semideviazione si calcola come la deviazione standard, eccetto che si modifica la formula per usare solo quei rendimenti che cadono al di sotto del rendimento medio del periodo.

Dove: RPi è l’i-esimo rendimento, la strana m (mi) è il rendimento medio aritmetico ed N è la numerosità dei rendimenti periodici (giornalieri, settimanali, mensili ecc) totali.
Procedimento operativo
- Si identificano i rendimenti che cadono al di sotto del rendimento medio.
- Si calcola la differenza tra questi rendimenti e il rendimento medio.
- Si eleva al quadrato ogni differenza.
- Si sommano (le differenze elevate al quadrato) ed infine la somma si divide per il numero totale dei rendimenti.
- Ciò ci dà la semivarianza.
- Facendo la radice quadrata della semivarianza, si converte la statistica in unità di rendimento, ciò significa che la statistica è direttamente confrontabile con i rendimenti.
Il folgio Excell illustra il calcolo della semideviazione. La semideviazione del fondo è 3,16% e la semideviazione del benchmark è uguale a 2,76%.
Osservazione 7> Nel calcolo della semideviazione il denominatore è il totale del numero delle osservazioni. Si sta calcolando la media delle deviazioni medie al di sotto della media, distribuite sul numero totale delle osservazioni. Qui, la divideremo in 13 mesi anche se solo 6 rendimenti cadono al di sotto del rendimento medio del fondo. La nostra formula è equivalente al calcolo della deviazione standard a parte il fatto che si mette 0 (zero) al posto delle deviazioni al di sopra della media.
Osservazione 8> Le metriche che considerano una porzione della distribuzione sono chiamate momenti parziali e le statistiche del rischio al ribasso sono momenti parziali inferiori. Usando i momenti parziali inferiori ci si rivolge alla critica riguardante la deviazione standard che misura allo stesso modo le deviazioni al di sopra della media, le quali potrebbero non essere considerate come rischiose allo stesso modo delle deviazioni al di sotto della media. Se una serie di rendimenti è distribuita normalmente, i fondi mostreranno la stessa rischiosità relativa se misurata con la deviazione standard o la semideviazione: ciò perché gli investimenti a grande deviazione al ribasso hanno anche una grande deviazione al rialzo. Se, comunque, la distribuzione dei rendimenti non è normale, la semideviazione e altre statistiche del rischio al ribasso trasmettono informazioni importanti come il downside risk dell’investimento. Nel caso della semideviazione, il ribasso viene misurato in relazione al rendimento medio, ma è possibile misurare il rischio al ribasso in relazione a qualsiasi punto della distribuzione di rendimento.
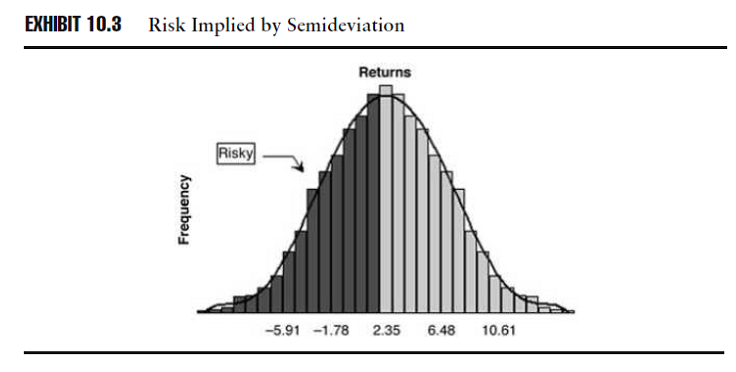
Fonte: Investment Performance Measurement (Bruce J. Feibel)
Rendimenti obiettivo
Osservazione 9> La seconda critica alla deviazione standard è quella che misura il rischio in relazione al rendimento medio, mentre gli investitori potrebbero considerare come rischiosi quei rendimenti che cadono al di sotto del presunto obiettivo di rendimento periodico. L’obiettivo può essere considerato un rendimento minimo accettabile, brevemente MAR (Minimum Acceptable Return), che ingloba ontologicamente i concetti secondo cui i rendimenti sopra il minimo sono accettabili e l’obiettivo di rendimento può essere differente dal rendimenti medio. Il MAR può essere considerato come un obiettivo di rendimento.
Il rendimento target sostituisce il rendimento medio come punto sulla distribuzione in cui si identificano i rendimenti considerati come rischiosi. Lo schema 10.4 mostra l’area della distribuzione considerata rischiosa se l’obiettivo di rendimento fosse uguale al 10%, in cui la media della distribuzione di rendimento è uguale al 13%.
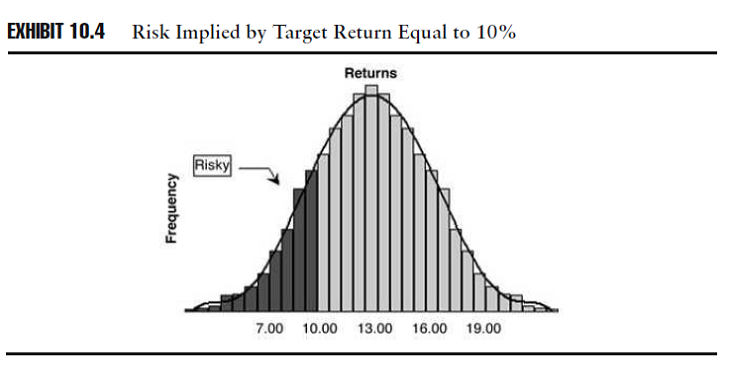
Fonte: Investment Performance Measurement (Bruce J. Feibel)
L’obiettivo di rendimento può essere considerato un rischio di benchmark personalizzato per in base alla tolleranza dell’investitore alle perdite periodiche. L’obiettivo di rendimento si concentra su obiettivi e scopi dell’investitore, e può essere o una percentuale fissa o un valore fluttuante che cambia ogni periodo.
Esempi di valore di obiettivo di rendimento:
- 0 (zero), che è il rendimento richiesto per mantenere normale il capitale. Usando un tasso 0 di percentuale di rendimento si assume di considerare qualsiasi perdita indesiderata nel valore di mercato.
- Il tasso attuariale di rendimento stimato usato per stimare i valori dei portafogli.
- Il rendimento risk free (privo di rischio), o rendimento dei T-bill.
- Il rendimento di un benchmark di mercato.
- Il rendimento maturato attraverso la competizione dei manager, come il terzo quartile rendimento universo dei manager.
È possibile usare diverse statistiche come metriche del rischio in relazione all’obiettivo di rendimento: shortfall risk, expected downside value (valore di ribasso atteso), deviazione in ribasso (Downside Deviation) e valore a rischio (Value at Risk). Poiché il tasso obiettivo di rendimento differisce tra investitori, la semideviazione e altre misurazioni di rischio al ribasso da noi esaminate non si trovano comunemente nelle statistiche pubblicate dei rendimenti o dei rischi ex-post di portafoglio.
Shortfall risk
Osservazione 10> Se la distribuzione di rendimenti fosse normale e noi definissimo rischio come semideviazione, ci aspetteremmo che il 50% dei rendimenti cadano sotto il rendimento medio. Se cambiassimo la view dal rendimento medio storico all’obiettivo di rendimento, potremmo misurare la remota probabilità dei rendimenti che cadessero al di sotto del valore designato. Questo shortfall risk è la percentuale dei rendimenti periodici che cadono al di sotto del valore designato: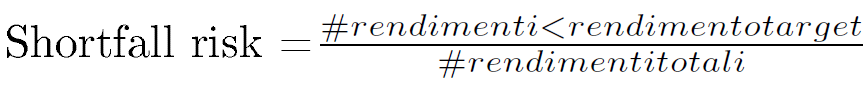
In altre parole è il numero dei rendimenti che cadono al di sotto del valore designato in un periodo, diviso per il numero totale di rendimenti riportati in percentuale. Esso misura la frequenza relativa di un fondo maturando un rendimento sotto al tasso di rendimento designato. Lo schema Excel mostra il calcolo dello shortfall risk usando un obiettivo di rendimento mensile dell’1,20%. Dato questo obiettivo, lo shortfall risk del nostro fondo è del 38,46% e il corrispondente shortfall risk del benchmark è lo stesso.
Questo tipo di rischio ci indica che il 38,46% dei rendimenti periodici mensili cadono sotto il nostro obiettivo di rendimento dell’1,20% al mese. Possiamo confrontare lo shortfall risk di fondi diversi per capire meglio come gli stessi soddisfino i bisogni dell’investitore circa il rendimento target. Questa metrica è anche usato per determinare l’asset allocation (=distribuire le risorse fra diversi i possibili investimenti).
Osservazione 11> Rappresenta una semplice statistica calcolata con una potente applicazione: essa mostra come rischiose le strategie che non sono normalmente considerate rischiose. Per esempio, un fondo dei buoni del tesoro non è normalmente classificato come investimento rischioso. Il capitale è protetto e il reddito è garantito. Guardando alla storia, sappiamo che i T-bill non sono probabilmente come il rendimento del nostro obiettivo di 1,2% al mese. Quindi, il nostro shortfall risk sarà vicino al 100% per il portafoglio T-bill.
Expected Downside value (Valore atteso a ribasso)
Osservazione 12> Lo shortfall risk quantifica la percentuale del tempo di un investimento che cade sotto un certo obiettivo, ma non dice nulla riguardo l’ampiezza del deficit. Il valore atteso al ribasso misura la quantità secondo cui un rendimento cade al di sotto dell’obiettivo di rendimento. La quantità di shortfall è mediata sul numero totale di osservazioni. Il valore atteso al ribasso si calcola usando la seguente equazione:
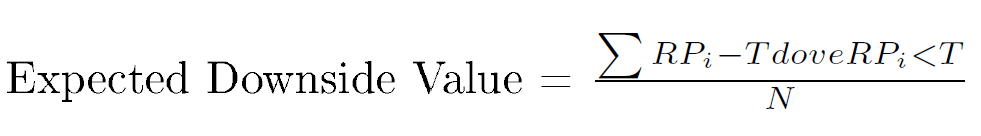
Dove T è il rendimento target; N= numero totale dei rendimenti
Supponiamo di avere una strategia che normalmente eccede l’obiettivo di rendimento, ma quando fallisce l’obiettivo si tratta di un ottimo affare ma breve.
Procedimento operativo:
- si identificano i rendimenti di fondo inferiori all’obiettivo di rendimento,
- si prende la differenza tra ognuno dei rendimenti e l’obiettivo di rendimento
- si aggiungono queste differenze.
- si divide la somma per il numero totale di investimenti produrre una deviazione media (ossia per calcolare la media del valore al ribasso lungo tutte le osservazioni).
Lo schema Excel mostra il calcolo del valore atteso al ribasso del nostro fondo e del benchmark di riferimento. Dato un obiettivo di rendimento mensile dell’1,2%, il valore atteso al ribasso è di 1,30% per il fondo e 1,37% per il benchmark. Il valore atteso al ribasso mostra che se il rendimento cade al di sotto dell’obiettivo di rendimento mensile dell’1.20%, cadrà sotto per una media dell’1,30% al mese.
Downside Deviation (Deviazione al ribasso)
Osservazione 13> La deviazione al ribasso, come la semideviazione, elimina dal calcolo del rischio i rendimenti che contribuiscono alla volatilità positiva. La deviazione al ribasso si calcola allo stesso modo della semideviazione, eccetto che per il fatto che si sostituisce il rendimento medio con il rendimento obiettivo.

Procedimento operativo:
- identificare i fondi con rendimenti minori dell’obiettivo
- prendere la differenza tra questi rendimenti e l’obiettivo
- si eleva questa differenza al quadrato
- si fa la somma di queste differenze quadratiche
- la si divide per il totale del numero dei rendimenti. Questo ci da la varianza al ribasso, o la semivarizanza sotto il target.
- Facendo la radice quadrata della varianza al ribasso si ottiene una statistica misurata unitaà di tasso di rendimento.
Il foglio Excell mostra il calcolo della deviazione al ribasso con un risultato del 2,55% per il fondo e 2,29% per il benchmark. È possibile annualizzare la deviazione al ribasso allo stesso modo della deviazione standard moltiplicando la deviazione al ribasso per la radice quadrata del numero delle osservazioni di rendimento dell’anno.
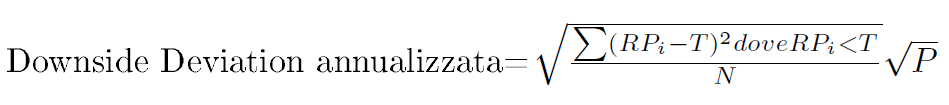
dove P è la periodicità delle osservazioni (rendimenti giornalieri => P = 250), o il numero delle osservazioni di rendimento nell’anno. Se si stanno usando i rendimenti mensili, la si moltiplica per la radice quadrata di 12.
Dato il target di rendimento mensile all’1,20%, la deviazione al ribasso annualizzata per il fondo è dell’8,82% e del 7,94% per il benchmark. Da ciò si evince che il fondo sperimenta più spesso rendimenti al ribasso relativamente al benchmark dato un obiettivo di rendimento dell’1.2% al mese.
Osservazione 14> Come tutte le statistiche che si calcolano nel processo di misurazione della performance, la deviazione al ribasso è calcolata usando la serie storica dei rendimenti dei fondi maturati nel periodo di tempo analizzato. Ciò fa si che la deviazione al ribasso sia molto sensibile al numero delle osservazioni di rendimento e al periodo selezionato. In sostanza, se i rendimenti di mercato sono genericamente positivi durante il periodo preso in esame, in seguito la deviazione al ribasso sarà attenuata, potenzialmente con grande impatto. Per affrontare questo problema, gli analisti hanno travato diversi metodi per calcolare il rischio al ribasso attraverso la simulazione della vera distribuzione dei rendimenti. Un metodo, chiamato metodo bootstrapping (o bootstrap), coinvolge la generazione di una distribuzione di rendimento ripetendo il campionamento (resampling, effettuato tramite montecarlo o metodo michaud, oggetto di trattazione in una futura analisi) di rendimenti periodici effettivi.
Osservazione 15> Il bootstrapping permette di generare un grande numero di possibili scenari nel calcolo del rischio al ribasso piuttosto che fare affidamento su un solo scenario, quale la serie storica effettiva. La determinazione del rischio al ribasso usando le simulazioni è più utile per la stima del rischio rivolto al futuro (looking-forward) piuttosto che calcolato usando i dati storici effettivi. In questo parte specifica della trattazione ci concentreremo sulla misurazione del rischio storico e misureremo il rischio al ribasso inerente alla serie storica effettiva dei rendimenti del fondo e del benchmark.
Nella prossima analisi misureremo il grado di rischio relativo: Il rischio relativo. Cosa è e come misurarlo tramite excel. Scopriamolo!
Come sempre spero di non aver fatto figuracce
Yours best
DF