Nel precedente articolo (Vedi: Calcolo dei rendimenti multiperiodo (aritmetici, geometrici) dei fondi tramite Excel) abbiamo illustrato la costruzione di metriche dei rendimenti multiperiodo; qui si vuole analizzare il rischio assoluto di un investimento e la distribuzione dei rendimenti (ricavati dai prezzi). Metriche quali la deviazione standard, i momenti centrali di ordine superiore al primo ed il VaR verranno presi in considerazione.
Si decide di investire tramite portafogli diversificati per massimizzare il rendimento che ci si aspetterebbe di ottenere data una particolare tolleranza del rischio.
Osservazione 1> La media, la deviazione standard e altre statistiche descrittive vengono usate appunto per descrivere il rischio assoluto (o meglio la distribuzione dei rendimenti) inerente alla sequenza dei rendimenti storici. Qui si farà una distinzione il rischio assoluto dalla misurazione del rischio, che si occupa di deviazioni dal rendimento di benchmark o target che sarà oggetto di trattazione futura. In tale sede, si illustra prima il calcolo e l’uso delle statistiche, le quali descrivono i rendimenti di una serie di periodi storici, e la misura della media, o rendimento medio, i cui rendimenti periodici sono variati; in seguito ci concentreremo sulle altre statistiche (o momenti centrali di ordine superiore al primo) misurandone il grado di variabilità intorno alla media.
Osservazione 2> la distribuzione, affinché la deviazione standard possa descrivere correttamente la variabilità in una serie di rendimenti, deve essere approssimativamente distribuita come una normale (vedi Markovitz sulla validità del modello).
La trattazione poi si chiuderà con una discussione riguardante le proprietà della distribuzione normale e le statistiche che indicano una deviazione dalla normalità.
Anche in tal caso, per completare il tutto e mettere mano con pratica, sarà presente un file Excel che mostra gli esempi di calcolo (spero, come sempre, di non fare figuracce…. 🙂 )
Range dei rendimenti
La volatilità dei rendimenti storici si nota analizzando il range dei rendimenti storici ottenuti. Possiamo sintetizzare la dispersione di una serie di rendimenti suddividendoli e prendendo la differenza tra il rendimento maggiore e minore al fine di calcolare il range dei rendimenti:
Range Rendimento= Rendimento maggiore – Rendimento minore
Il range è la differenza tra il rendimento maggiore e minore ottenuti. Il rendimento maggiore e minore, nel nostro esempio corrispondono a -7,00% e -3,00% e la varietà è uguale a 10,00%. Il confronto tra range è una rappresentazione facile da computare e comprendere della relativa volatilità di due fondi.
Distribuzione dei rendimenti
Il problema dei range è che sono altamente impattati dalle deviazioni estreme. Per esempio, il range di un rendimento annuale del T-bill (buoni del tesoro) nel periodo che va dal 1926 al 2000 era pari a differenziale tra il -0,02% e il 14,71%. Tuttavia, il rendimento a -0,02% del 1938 fu il solo rendimento negativo maturato; il rendimento del 14,71%, invece, si verificò nel 1981, l’unico anno in cui i rendimenti T-bill furono più elevati dell’11,24%. Facendo uso dei range dei rendimenti per stimare il rischio si escludono le informazioni riguardanti la probabilità storica di ottenere un particolare livello di rendimento. Spesso il miglior modo per comprendere la dispersione di rendimenti e la loro relativa frequenza, è di visualizzare la distribuzione di rendimenti tramite un grafico. Raggruppando i rendimenti in ragne, è possibile rappresentare la distribuzione di frequenza, o istogramma, dei rendimenti. L’istogramma mostra la frequenza relativa (in %) con la quale i rendimenti cadono in diversi range di rendimenti -o classi di intervalli-.
L’istogramma si forma dividendo una serie di rendimenti in un numero di intervalli. Se sono presenti troppi pochi intervalli, la forma della distribuzione del rendimento non potrà essere raffigurata dal grafico. Maggiore è il numero, più accuratamente il grafico potrà rappresentare la distribuzione del rendimento. Ma se si aggiungono più contenitori, i vuoti inizieranno ad apparire dove saranno presenti intervalli senza rendimenti. Una volta che si è deciso il numero che rappresenta nel miglior modo la distribuzione evidenziata, si sottrae il valore leggermente superiore al rendimento minore dal valore leggermente inferiore del rendimento maggiore per poi dividere la differenza per il numero dei contenitori. Da questo calcolo si ricavano gli intervalli tra i contenitori. Si creeranno poi i contenitori aggiungendo gli intervalli iniziando dal rendimento minore.

Fonte: Investment Performance Measurement (Bruce J. Feibel)
Lo schema 9.1 rappresenta l’istogramma dei rendimenti del nostro fondo e del benchmark. Anche se in una situazione reale esiteremo a trarre conclusioni basate su rendimenti di 13 mesi, possiamo comunque vedere una simile distribuzione di rendimenti da entrambi i redditi. Un istogramma di rendimenti di azioni americane a larga capitalizzazione mensile dal Gennaio 1971 a Dicembre 2000, mostrato nello schema 9.2, è più esplicativo.
Osservazione 3> i rendimenti si raggruppano attorno al rendimento medio di approssimativamente l’1% al mese. Anche la frequenza dei rendimenti maturati diminuisce nel momento in cui si muovono verso il limite alto o basso, eccetto se lo alziamo ancora verso qualunque limite (positivo o negativo).
Deviazione dei rendimenti
Mentre l’istogramma fornisce una rappresentazione grafica della dispersione in rendimenti, in qualsiasi analisi finanziaria abbiamo bisogno di statistiche sintetiche per descrivene la dispersione. Lo schema 9.2 è un esempio di un fenomeno in cui i rendimenti della maggior parte delle strategie di investimento tendono a una media.
Il foglio 1 mostra il calcolo del rendimento medio aritmetico mensile, dove 2,35% corrisponde al nostro fondo di riferimento e 1,98% al benchmark. In media, il fondo supera il benchmark per lo 0,37% al mese.
Abbiamo mostrato il calcolo del rendimento medio usato durante la misurazione del rischio allo scopo di differenziare il rendimento medio aritmetico dal rendimento medio geometrico. Il rendimento medio geometrico è la misurazione base della performance di un investimento. Esso computa l’effetto compounding dei rendimenti che si verifica quando gli interessi maturati in un periodo sono investiti nei periodi successivi. Esso può essere usato per giustificare il valore iniziale di un investimento con il valore finale. Specularmente, il rendimento medio aritmetico è una semplice media dei rendimenti periodici. È un rendimento rappresentativo che, raggruppando ogni osservazione del rendimento in un unico numero, vuole essere rappresentativo delle serie storiche dei rendimenti. Il rendimento medio aritmetico non tiene conto dei reinvestimenti degli introiti e redditi periodici. Per questo motivo esso sarà maggiore o uguale, al rendimento geometrico.
Osservazione 4> il rendimento medio aritmetico è comunque utile nell’analisi della distribuzione dei rendimenti periodici che implica il rischio di investimento perché fornisce il centro attorno al quale i rendimenti periodici osservati sono distribuiti. Comunque, con alcune rettifiche agli input, i rendimenti geometrici possono anche essere usati nella misurazione del rischio storico. A vantaggio della coerenza useremo, in questo libro, i rendimenti aritmetici negli esempi dimostranti la misurazione del rischio.
Osservazione 5> un problema con la media è che, analogamente ai range, è altamente impattata dalle deviazioni estreme -ossia che sono osservazioni lontane dal rendimento medio-. Talvolta il calcolo della media che include le deviazioni estreme può dare un’impressione fuorviante visto che il rendimento medio è maturato lungo un determinato periodo. Un metodo per calcolare una media che eviti il problema della deviazione estrema è computare una media ridotta. Una percentuale delle deviazioni maggiori e minori vengono escluse dal calcolo della media ridotta.
Mean Absolute Deviation, MAD (Deviazione Media Assoluta)
Sarebbe bene se noi trovassimo una singola statistica che includa l’idea della gamma ma che eviti il problema delle deviazioni tenendo in considerazione tutte le deviazioni dal rendimento medio invece che solo le due deviazioni più grandi, come nella gamma. Un modo intuitivo per cercare di includere in una singola statistica la totale variabilità di una serie di rendimenti sarebbe quella di prendere la media di tutte le deviazioni di rendimenti. Comunque, non possiamo prendere la semplice media perché la somma delle deviazioni dei rendimento è 0. Per correggere ciò, possiamo invece prendere il valore assoluto delle deviazioni e calcolarne la media. La media del valore assoluto delle deviazioni di rendimento è chiamata Deviazione media assoluta (MAD) o Deviazione media.
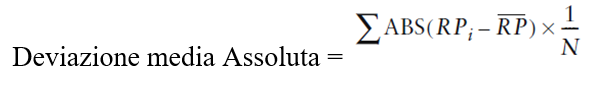
La deviazione media assoluta è la media aritmetica del valore assoluto della differenza tra ogni rendimento registrato e la media aritmetica dei rendimenti. Non farti spaventare dalle formule, in excel troverai l’algoritmo di calcolo illustrato nel modo più semplice possibile (usando a volte built in function, usando a volte il calcolo passo passo). Nello schema (foglio 1) il calcolo della deviazione media assoluta del nostro fondo e benchmark corrispondono rispettivamente a 3,54% e 3,35%.
Osservazione 6> usando la deviazione media assoluta possiamo vedere che, anche se il fondo ha un rendimento medio aritmetico maggiore lungo nel periodo analizzato, ha anche una dispersione di rendimenti maggiore intorno alla media. Visto che stiamo utilizzando la variabilità nei rendimenti come surrogato del rischio, questa è la nostra prima indicazione che magari il fondo sia più esposto al rischio lungo il lasso di tempo osservato.
Deviazione Standard
Nonostante la deviazione media assoluta sia una descrizione funzionale della variabilità in una serie di rendimenti, non viene usata spesso nell’analisi della performance. Ciò in quanto esistono misure della variabilità dei rendimenti con proprietà statistiche migliori rispetto alla deviazione media assoluta, e che trasmettono le stesse informazioni. Useremo le deviazioni dalla media nel calcolo delle dispersioni di rendimenti, ossia la deviazione standard dei rendimenti. La deviazione standard è la misura di quanto ampiamente i rendimenti effettivi siano dispersi dal rendimento medio aritmentico: invece di prendere il valore assoluto di ogni deviazione, si eleva al quadrato ogni deviazione. Ciò ha lo stesso effetto (pesa ugualmente i rendimenti positivi e negativi) come se avessimo preso il valore assoluto per mezzo del quale tutte le deviazioni vengono cambiate in numeri positivi. Le deviazioni elevate al quadrato vengono sommate e poi divise per il numero di rendimento per ottenere la varianza. Noi tipicamente evitiamo di usare la varianza come misura del rischio ex-post perché viene misurato in rendimenti elevati al quadrato, piuttosto che dai rendimenti. In altre parole, non è possibile confrontare direttamente la varianza con il rendimento allo scopo di valutare la remunerazione al rischio.
Osservazione 7> È possibile, comunque, confrontare la deviazione standard con i rendimenti per fare una confronto diretto La deviazione standard è la radice quadrata della varianza.
Procedimento operativo:
- elevare al quadrato ogni differenza tra i rendimenti periodici e il rendimento medio aritmetico;
- calcolare la differenza elevata al quadrato
- dividere il totale delle differenza elevata al quadrato per il numero dei rendimenti;
- calcolare la radice quadrata del risultato.
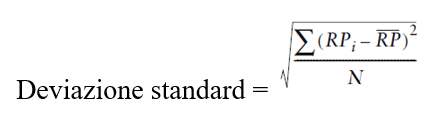
Dove: RPi è l’osservazione dei rendimenti individuali del portafoglio, RP soprasegnato è il rendimento medio aritmetico e N è la somma dei rendimenti.
Osservazione 8: il fatto che stiamo elevando al quadrato le deviazioni implica che la deviazione standard è influenzata più dalle deviazioni estreme (outliers) rispetto alla deviazione media assoluta.
Lo schema excel (foglio 1) illustra il calcolo della deviazione standard del nostro fondo, uguale al 4,13%. La deviazione standard del benchmark è inferiore, è 3,65%.
La deviazione standard è la prima statistica usata per descrivere la variabilità nel modello dei rendimenti, e visto che la varianza è “delegata” del rischio la deviazione standard dei rendimenti periodici è “delegata” del rischio usato nella gestione e nell’analisi d’investimento. Una maggiore deviazione standard indica una più grande dispersione dei rendimenti intorno al rendimento medio. Un portafoglio che raddoppia la deviazione standard di un altro fondo, raddoppia anche la volatilità come quella del fondo.
Osservazione 9> esistono poche considerazione che dovremmo ricordare quando si utilizza la deviazione standard e le relative misure del rischio; queste includono il numero delle osservazioni usate per formare la statistica e la periodicità dei dati usati sottostante.
Lunghezza del periodo
Osservazione 10> gli esempi di questa sezione del libro utilizzano i rendimenti mensili di 13 mesi come input, un piccolo numero di osservazioni per facilitare lo studio del calcolo e dell’interpretazione delle varie statistiche. Un’analisi pratica, comunque, coinvolgerà usualmente periodi di tempo più lunghi. Ma quante osservazioni di rendimento utilizzeremo? I professionisti usano spesso 3 anni di dati mensili o 36 osservazioni mensili per analizzare il rischio storico della strategia d’investimento.
La scelta del periodo di tempo implica sia il numero delle osservazioni usate sia la rilevazione di tutte le fasi del ciclo di mercato. Se avessimo un periodo di tempo corto, le statistiche sarebbero maggiormente instabili visto che le stesse sono sensibili all’aggiunta o alla sottrazione di addizionali periodi. I risultati avranno una bassa validità statistica. Inoltre, se arrivassimo a conclusioni basate ad esempio sulla deviazione standard, le stesse potrebbero essere non valide se il periodo di tempo non rappresentasse diverse fasi dei ciclo di mercato: nel nostro caso, i periodi con alta e bassa volatilità. Qui stiamo anche implicitamente ponderando equamente ogni osservazione di rendimento quando calcoliamo il rischio statistico. Per esempio, se stiamo calcolando la deviazione standard tracciata in 3 anni, il rendimento di 36 mesi fa contribuirà egualmente al calcolo allo stesso modo dell’ultimo rendimento del mese. Ci sono delle alternative alla equa ponderazione, per esempio, usando le medie mobili ponderate, in cui il periodo più recente avrà un maggiore peso nel calcolo. Utilizzeremo le tecniche di ponderazione nelle stime ex ante, o del rischio futuro, rispetto alla misurazione del rischio storico.
Osservazione 11> un problema correlato è l’utilizzo del versione campionaria rispetto a quella dell’intera popolazione e della deviazione standard. Quando si ricavano le medie usate nel rischio statistico, come la media delle deviazioni di rendimento utilizzate nelle deviazioni standard, si dividono per il numero totale dei rendimenti nel set di dati, o N: dividendo per N si ricava la media, quando stiamo calcolando il rischio statistico dell’intera popolazione, dei rendimenti che vogliamo rappresentare. Quando utilizziamo le statistiche come la deviazione standard per identificare le caratteristiche di un completo set di dati, utilizzeremo la versione campionaria di queste statistiche. Qualche volta è possibile calcolare il rischio statistico usando una parte della popolazione, o un set di campioni di rendimenti. Quando si calcola il rischio statistico tramite un campione,usando le statistiche per valutare l’intera popolazione, lo si divide per N-1 invece che per N. Se ricalcolassimo gli esempi di questo capitolo dividendoli per N-1 invece che per N, avremo significativi risultati assoluti diversi. Questo perché abbiamo scelto di usare solo 13 osservazioni per facilitare lo studio di ogni misurazione. La rettifica dei campioni non è una considerazione rilevante nell’analisi del rischio, perché si utilizza usualmente una quantità abbastanza grande di osservazioni di rendimenti che, divisi o per N o per N-1, dà approssimativamente lo stesso risultato. In ogni caso, nessuna delle relative classifiche e inferenze fatte basate sulla differenza tra il rischio del fondo e quello del benchmark sarebbero mutate. Se prendessimo il rischio statistico calcolato usando due fondi differenti e poi li confrontassimo, sarebbe utile per noi sapere se fosse stata usato il metodo campionario o della popolazione.
Frequenze di misurazione
Osservazione 12> se stessimo calcolando giornalmente il TWR di singoli periodi, per calcolare un rendimento cumulativo di un anno potremmo collegare o i rendimenti cumulativi di circa un anno o i rendimenti di 12 mesi. In ogni caso otterremo lo stesso rendimento di un anno perché il TWR può essere compresso: i rendimenti giornalieri di un mese sono uguali al rendimento mensile e così via. Questa proprietà non la si può estendere alla misurazione del rischio. La periodicità dei rendimenti influenza il calcolo del rischio!
Per esempio, visto che i rendimenti usualmente fluttuano meno in un giorno che in un mese, la deviazione standard di una serie di rendimenti giornalieri è di solito più contenuta rispetto alla deviazione standard di rendimenti mensili lungo lo stesso periodo. Il rischio statistico viene comunemente calcolato usando rendimenti periodici con frequenze giornaliere, settimanali, mensili o trimestrali. È inappropriato confrontare il rischio statistico che sarebbe stato calcolato usando una periodicità differente. La scelta della frequenza dei rendimenti dipende dalla disponibilità dei dati dei rendimenti dei fondi considerati, la quale a sua volta è dipendente dalla periodicità -o frequenza- della valutazione. Tradizionalmente, la valutazione è solo disponibile su base mensile per molti veicoli d’investimento, eccetto per i fondi comuni d’investimento. Visto che le valutazioni dei portafogli d’investimento stanno diventando prevalentemente esterni dal fondo comune d’investimento, la frequenza giornaliera della misurazione del rischio è ora possibile. Ipotizzando di misurare il rischio su base giornaliera, il rischio statistico calcolato usando input mensili non rappresenterebbe il rischio sotto inteso dal rendimento giornaliero. Inoltre, è possibile che le classifiche relative dei portafogli o delle strategie cambierebbero con maggiore o minore frequenza dei dati. L’uso delle osservazioni giornaliere permette di misurare la vera volatilità maturata dall’investitore.
Rischio statistico geometrico vs aritmetico
Finora abbiamo calcolato la deviazione standard dei rendimenti periodici intorno al rendimento medio aritmetico. Potremo invece calcolare la deviazione standard dei rendimenti intorno al rendimento medio geometrico. Per fare ciò bisogna prima calcolare il logaritmo naturale dei tassi di crescita dei rendimenti di singoli periodi, e poi prendere la deviazione standard di questi tassi di crescita.
Osservazione 13> pratica molte comune nelle analisi è usare la metodologia aritmetica per calcolare il rischio storico statistico, ma anche le statistiche geometriche sono valide.
Deviazione standard annualizzata
Per la stessa ragione per cui è utile convertire il rendimento in equivalenti annuali possiamo convertire il rischio su una base annua. Il metodo per annualizzare i rischi è differente da quello usato per annualizzare i rendimenti. La versione annualizzata della statistica della deviazione standard è spesso chiamata volatilità. Per annualizzare la deviazione standard, si deve moltiplicare la deviazione standard per la radice quadrata del numero dei rendimenti in un anno data la periodicità dei dati.

dove P è il numero dei periodi di rendimenti per anno: se freq=giornaliera allora P=250, se freq=mensile allora P=12, se freq= 2 anni allora P=1/2.
Osservazione 14> l’esempio Excel usa i dati mensili quindi abbiamo moltiplicato la deviazione standard dei rendimenti mensili (4,13%) per la radice quadrata di 12, che è approssimativamente 3,46, allo scopo di annualizzare i rendimenti. la deviazione standard annuale del nostro esempio è 14,32% per il fondo e 12,63% per il benchmark. Se le osservazioni del rendimento sono trimestrali le moltiplicheremo per la radice quadrata di 4, se sono settimanali per 52 e se sono giornaliere per la radice quadrata del numero dei giorni di negoziazione in un anno del mercato in cui stiamo investendo (circa 250 giorni di borsa aperta).
Si moltiplica la deviazione standard per la radice quadrata della periodicità necessaria a trasformare la statistica periodica in una statistica comparabile con il rendimento annuale aritmetico. In questo esempio, utilizzeremo i rendimenti mensili per calcolare il rendimento medio mensile. Calcoleremo poi l’equivalente annuale del rendimento medio aritmetico moltiplicando il rendimento medio aritmetico periodico per il numero di rendimenti in un anno, dato dalla frequenza dei dati. Moltiplicheremo infine il rendimento medio aritmetico mensile per 12 per calcolare il rendimento medio aritmetico annuale equivalente.
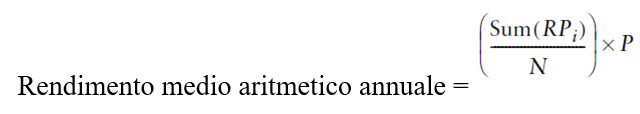
dove P è il numero dei periodi di rendimento per anno o periodicità dei rendimenti. È il rendimento medio aritmetico annuale che fa variare la deviazione standard dei rendimenti aritmetici.
Osservazione 15> I rendimenti medi annuali nel nostro esempio corrispondo al 28.25% per il fondo e 23.80% per il benchmark. Se le osservazioni di rendimento fossero trimestrali moltiplicheremmo la media trimestrale per 4, quella settimanale per 52 e quella giornaliera per il numero dei giorni di negoziazione che si sono verificati durante l’anno. Ciò corrisponde approssimamente a 250, ma dipende dal programma di vacanze del mercato in cui si sta negoziando.
Abbiamo preso il rendimento mensile e lo abbiamo moltiplicato per 12 per il computo del rendimento medio annuale. Allo stesso modo, potremo prendere la varianza mensile e moltiplicarla per 12 per calcolare la varianza annuale. Visto che la deviazione standard è la radice quadrata della varianza, sarebbe coerente moltiplicare la deviazione standard per la radice quadrata di 12 per formare l’equivalente annualizzato. Questo metodo di conversione è spesso chiamato regola della radice quadrata del tempo, con cui si ipotizza che il rischio si formi con la radice quadrata del tempo.
Osservazione 16> questa regola non è sempre valida. Diversi studi riguardanti asset class differenti, sono giunti a risultati in cui la varianza aumenta di più o di meno rispetto alla deviazione standard del tempo. Per esempio, la deviazione standard dei rendimenti giornalieri composta da serie annuali usando la regola della radice quadrata, potrebbe sovrastare o sottostare la deviazione standard visto che viene calcolata usando input mensili.
Usando i rendimenti del mercato come esempio, la deviazione standard mensile di azioni americane a grande capitalizzazione risulterebbe approssimativamente al 4,43% dal 1971 al 2000. L’equivalente annuale corrisponderebbe a 15,33% (4,43% moltiplicato per 3,46); la deviazione standard dei rendimenti annuali dello stesso periodo è effettivamente un po’ più alta, circa pari al 15,84%. In altri casi la volatilità sarà più alta nei periodi a breve termine rispetto a quelli a lungo temine, ossia, la deviazione standard di rendimenti mensili composta da equivalenti annuali sarà maggiore rispetto alla deviazione standard dei rendimenti annuali.
Osservazione 17> la regola della radice quadrata del tempo presuppone che i cambiamenti nella serie di rendimenti siano casuali, ossia che i rendimenti periodici non siano correlati in serie. La correlazione seriale è un indicazione secondo cui esiste una tendenza nelle serie temporali dei rendimenti: se correlati positivamente a rendimenti positivi dovrebbero susseguire rendimenti positivi o negativi nel caso speculare; se correlati inversamente è probabile che a rendimenti positivi susseguano rendimenti negativi e viceversa; se non correlati non esiste nessun pattern. Se i rendimenti mostrano una correlazione seriale, allora utilizzando la regola della radice quadrata del tempo per stimare il rischio nei multi periodi, si sottovaluterà il rischio effettivo.
NB: Esistono altri metodi per ridimensionare il rischio in presenza di una correlazione seriale!
Distribuzione normale
L’istogramma mostra come i rendimenti osservati sono distribuiti intorno al rendimento medio. I rendimenti sono statistiche continue, ossia, possono prendere qualsiasi valore all’interno della gamma di rendimenti.
Osservazione 18> I rendimenti sono normalmente distribuiti quando le osservazioni di rendimento ugualmente distanti dal rendimento medio hanno la stessa frequenza relativa dell’osservazione: è una distribuzione simmetrica).
In una serie di rendimenti normalmente distribuiti, la maggior parte dei rendimenti sono vicini al rendimento medio e i rendimenti estremamente alti o bassi sono relativamente pochi. La distribuzione normale può essere descritta con un’equazione che calcola l’area sotto la curva a campana (equazione intergrale), e che può essere disegnata in un istogramma di una popolazione normalmente distribuita di rendimenti. Lo schema 9.7 illustra la serie di un rendimento con una normale distribuzione.
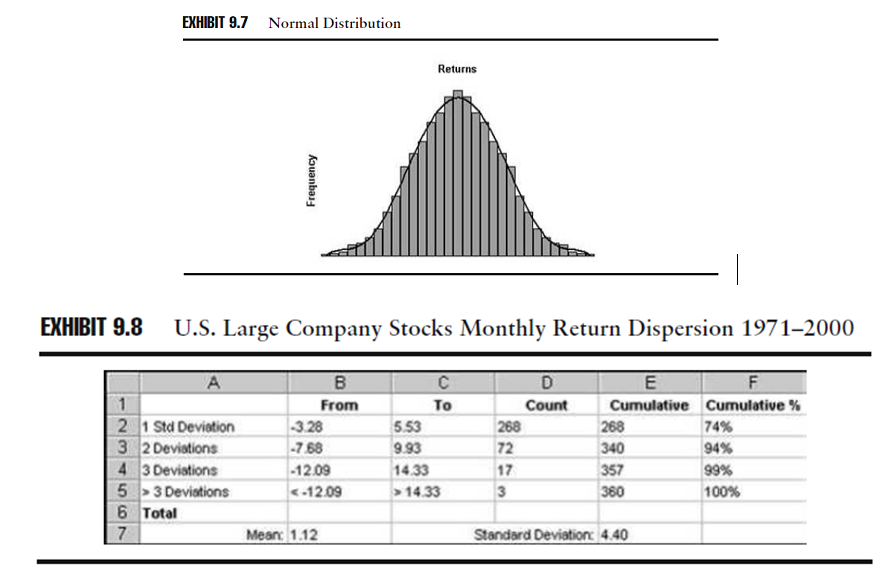
Fonte: Investment Performance Measurement (Bruce J. Feibel)
La distribuzione normale è una descrizione accurata della dispersione di valori intorno alla media per molte cose, come le altezze e il peso di gruppi di persone.
Una proprietà della deviazione standard per una normale distribuzione della popolazione è che è possibile usare la deviazione standard insieme alla media per descrivere matematicamente la distribuzione di serie temporali di rendimenti, come evidenziate dall’istogramma:
- Circa il 68% dei rendimenti osservati saranno all’interno della gamma di 1 deviazione standard superiore o inferiore al rendimento medio;
- Circa il 95% dei rendimenti sarà all’interno del ± 1.65 delle deviazioni standard;
- Circa il 97,5% dei rendimenti sarà all’interno del ± 1,96 delle deviazioni standard;
- Quasi tutti i rendimenti saranno all’interno del ± 3 delle deviazioni standard.
Diamo un’occhiata alla storia dei rendimenti delle azioni americane a larga capitalizzazione mensile per esaminare queste regole empiriche. Il rendimento medio mensile del periodo fra Gennaio 1971 e Dicembre 2000 corrispondeva all’1,12% e la deviazione standard era di 4,40%.
Osservazione 19> lo schema 9.8 (vedi sopra) mostra che la dispersione dei rendimenti delle azioni americane a larga capitalizzazione mensile si avvicina alla distribuzione descritta dalla normale distribuzione. È interessante il fatto che ci siano 3 mesi, che potremo chiamare eventi estremi, in cui i rendimenti erano più di 3 distribuzioni lontane dal rendimento medio. In questo caso, erano tutti nel lato negativo (Ottobre 1974 -16.57%, Ottobre 1987 -21.52% e Agosto 1998 -14.46%). La deviazione standard dei rendimenti, senza includere questi mesi, è di 4.09%. Questo mostra come le deviazioni estreme influenzino la deviazione standard.
Osservazione 20> Quando utilizziamo le regole empiriche insieme alla deviazione standard, si sta assumendo di utilizzare la distribuzione normale per determinare la probabilità di maturare rendimenti particolari diversi dal rendimento medio. Sono proprio queste probabilità che rappresentano il rischio d’investimento.
Valore a rischio storico, Historical Vaue at Risk (H-VaR)
Un modo per utilizzare la distribuzione normale è quello di convertire la percentuale di rischio in rischio di dollari. Quando stiamo comunicando i rischi associati ad un investimento, ergo è utile convertire la deviazione standard in termini percentuali in termini di denaro.
Osservazione 21> Il Valore a rischio (VaR) è una stima della perdita di denaro massima che potremo aspettarci, in un dato orizzonte temporale, con un certo livello di confidenza (probabilità). VaR è la perdita di denaro in una particolare posizione percentile di una distribuzione di rendimenti.
Per esempio, supponiamo di avere un portafoglio con un valore al momento di €100,000. Avendo un VaR mensile di €10,000 con un livello di confidenza di circa il 5%, interpreteremo questo per dire “non ci aspettiamo perdite maggiori del 10% (10.000/100.000) del valore del portafoglio in più di 1 mese e meno di 20 mesi”. Il VaR è espresso in termini di valore in denaro del portafoglio, per tal motivo per molti investitori è più una misura intuitiva del rischio piuttosto che una deviazione standard.
Per calcolare il VaR, bisogna prima selezionare un livello di confidenza. Per esempio, se si vuole affermare con certezza che il 95,05% delle perdite in un particolare periodo, non scendono al di sotto di un certo livello, si dovrebbero considerare rischiosi quei rendimenti la cui deviazione standard è caduta 1,65 volte al di sotto del rendimento medio, come indicato dallo schema Excell
Abbiamo scelto la deviazione standard 1,65 perché ci aspettavamo che circa il 95% dei rendimenti cadesse all’interno delle deviazioni standard ±1.65 dalla media. Il 10% è diviso tra la coda più alta e più bassa della distribuzione; questo è: il 5% dei rendimenti sono previsti che cadano nella deviazione standard 1,65 sotto la media e il 5% dei rendimenti della deviazione standard 1.65 sopra la media. Dato il livello di confidenza, è possibile determinare il VaR storico moltiplicando un investimento ipotetico realizzato per il rendimento al punto in cui la distribuzione 1,65 delle deviazioni standard è sotto il rendimento medio. L’equazione mostra come è possibile calcolare ciò usando la deviazione standard dei rendimenti.
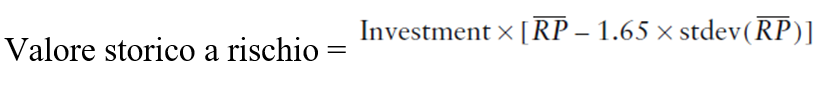
Lo schema Excel illustra il calcolo del VaR del nostro fondo e benchmark preso in considerazione. Possiamo vedere che con un investimento di €10,000 in un fondo ci aspetteremo di perdere non più di €446,82 in un qualsiasi mese, 95% del periodo.
Questo significa che per il 95% del periodo ci aspetteremo di ottenere un fondo di rendimento mensile uguale a o maggiore a –4,47%. Si calcola il rendimento ad 1,65 volte la deviazione standard sotto la media moltiplicando la deviazione standard per 1,65 e sottraendo poi il risultato dal rendimento medio, il quale è al punto 0 (zero) delle deviazioni standard. Ricaveremo il VaR in termini € moltiplicando il risultato per l’investimento iniziale di €10,000. Il VaR non implica che questo è il rendimento più basso ottenuto; ci aspetteremo che il 5% dei rendimenti periodici cadano sotto questa cifra con una grande perdita di denaro.
Osservazione 22> Il metodo per calcolare il VaR qui trattato è un’applicazione della deviazione standard nella misurazione del rischio assoluto rivolto al passato (backward-looking). Il VaR è più comunemente usato su una base rivolta al futuro (forward-looking). Un modo di calcolare questo tipo di VaR è quello di prendere gli investimenti effettivi del portafoglio, le stime riguardanti la variabilità di rendimento e la correlazione di rendimento tra questi investimenti, per generare una distribuzione di possibili valori di mercato futuri. Produrremo le stime della correlazione e variabilità futura facendo affidamento sulla storia come guida ed esistono molti metodi per fare questo.
Altre distribuzioni
Osservazione 23!> Una precisazione sull’utilizzo del VaR calcolato usando la media e la deviazione standard: stiamo ipotizzando che i rendimenti siano distribuiti normalmente. Per usare la regola empirica associata alla deviazione standard, ossia il 95% dei rendimenti attesi all’interno della gamma di una deviazione standard sopra o sotto la media, i rendimenti individuali necessitano di essere ragionevolmente distribuiti normalmente attorno al rendimento medio.
Osservazione 24> La distribuzione normale è disposta simmetricamente intorno al rendimento medio. La serie storica del rendimento potrebbe avere un numero maggiore di rendimenti estremamente alti o bassi rispetto a quanto indicherebbe la distribuzione normale. Alcune strategie d’investimento sono designate per produrre asimmetricamente, o non normalmente, le distribuzioni di investimento. Le strategie che impiegano opzioni di contratto sono esempi di investimenti che producono una distribuzione non normale. Per esempio, l’uso di opzioni put acquistate attenua il rischio di perdite, mentre si lascia il potenziale di guadagni, in cambio di un rendimento medio più basso che riflette il costo delle opzioni put. Le opzioni call scritte hanno l’effetto opposto. Il potenziale di rialzo dei fondi è troncato nello scambio delle opzioni premium in aumento nei rendimenti medi. Esistono molti altri esempi di strategie designate per produrre una distribuzione di rendimento non normale. In questi casi la distribuzione di rendimenti è asimmetrica. Inoltre, la distribuzione di rendimento prenderebbe forme diverse a seconda della frequenza di osservazione o del periodo che si sta misurando. Ci sono insiemi di altre possibili distribuzioni che una serie di rendimenti potrebbero contenere. Avendo detto ciò, molte strategie sono servite alla deviazione standard perché il modello delle strategie si avvicina ad una distribuzione normale, o lognormale.
Osservazione 25> La deviazione standard non è una descrizione accurata della dispersione di rendimenti in cui la distribuzione di rendimento è asimmetrica. Un segnale che la distribuzione di rendimenti potrebbe essere non normale è quando il rendimento mediano è maggiore o minore rispetto al rendimento medio. Il rendimento mediano è il rendimento intermedio in una varietà di rendimenti ordinata dall’alto verso il basso. Per una distribuzione simmetrica perfetta, la distribuzione media e mediana sono quasi uguali. Due modalità importanti per le quali una distribuzione di rendimento dovrebbe essere non normale sono la distribuzione che esibisce asimmetria o curtosi. È possibile misurare queste proprietà per determinare se la distribuzione è normale o no.
Momenti centrali di ordine superiore al secondo
Oltre a media e varianza, rispettivamente momenti centrali di ordine 1 e 2 della distribuzione, esistono momenti di ordine superiore: la a/simmetria e la curtosi
Skewness (a/simmetria)
Se ci sono più rendimenti nella parte destra della distribuzione del rendimento storico (=più del normale), possiamo dire che la distribuzione è inclinata positivamente a destra come si vede nello schema 9,11.
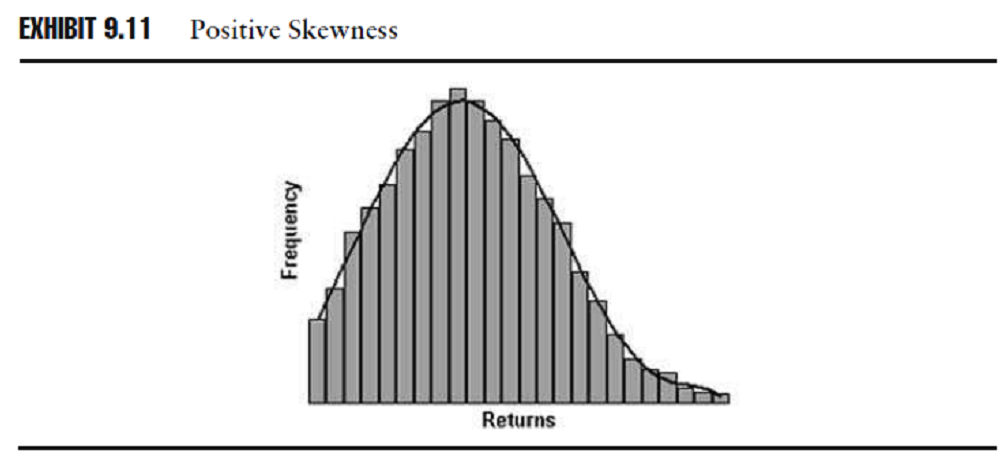
Fonte: Investment Performance Measurement (Bruce J. Feibel)
Osservazione26> L’istogramma di una distribuzione inclinata positivamente ha più rendimenti estesi sulla parte destra rispetto ad una distribuzione normale. Se i rendimenti sono inclinati positivamente, il rendimento medio è maggiore rispetto al rendimento mediano (ossia che “spacca” a metà la distribuzione) a causa dell’effetto che la deviazione estrema positiva ha sulla media. Se i rendimenti sono inclinati positivamente, la deviazione standard sottovaluterà la proporzione dei rendimenti sopra la media ma la sopravvaluterà sotto la media.
Il fatto che ci siano rendimenti più estesi sulla parte sinistra della distribuzione di rendimento (= più rispetto ad una distruzione normale) implica che la distribuzione è inclinata negativamente, come nello schema 9.12.

Fonte: Investment Performance Measurement (Bruce J. Feibel)
Osservazione 27> L’istogramma del rendimento inclinato negativamente sembra che abbia una coda che si estenda sulla destra. Se i rendimenti sono inclinati negativamente, il rendimento mediano sarà maggiore del rendimento medio a causa dell’effetto che la deviazione estrema positiva ha sulla media. Se i rendimenti sono inclinati positivamente, la deviazione standard sopravvaluterà la proporzione dei rendimenti sopra la media ma la sottovaluterà sotto la media. Questo è molto importante perché stiamo usando la deviazione standard come misura di rendimenti con incertezza. Se la serie di rendimenti ha un’asimmetria negativa, possiamo sottovalutare il rischio al di sotto del rendimento medio usando la deviazione standard per descrivere la dispersione dei rendimenti.
Quello che si vuole misurare è il grado di asimmetria presente nella distribuzione di rendimenti per stimare la normalità, ergo l’appropriatezza della deviazione standard come una descrizione della variabilità. La statistica asimmetrica è la misura del grado di asimmetria dei rendimenti attorno alla media. È possibile misurare il grado di asimmetria usando:

Procedimento operativo (consiglio: utilizzare anche built-in function per facilitare il lavoro):
- calcolare la differenza tra ogni rendimento mensile e il rendimento medio aritmetico.
- dividere la differenza per la deviazione standard dei rendimenti.
- elevare il risultato al cubo.
- sommare le differenze al cubo.
- dividere la somma delle differenze al cubo per il totale dei rendimenti.
Lo schema excell illustra il calcolo di asimmetria uguale a -0.44 del nostro fondo e -0,32 del nostro benchmark preso come riferimento.
Osservazione 28> Una distribuzione perfettamente normale del rendimento ha un’asimmetria pari a 0. Sfortunatamente, l’asimmetria non viene misurata in unità di rendimenti, come la deviazione media e standard.
La statistica asimmetrica può solo essere interpretata come una misura della forma della distribuzione del rendimento. Più alto è il valore assoluto dell’asimmetria più la serie di rendimenti tenderà verso la coda più alta o più bassa della distribuzione normale. Se la distribuzione di rendimento è inclinata verso la coda destra, l’asimmetria sarà positiva. L’asimmetria positiva ci dice che esistono deviazioni estreme di rendimenti positive. In altre parole, l’asimmetria positiva indica che quando ci sono dei guadagni saranno maggiori di quanto immaginato, e le perdite saranno più piccole rispetto a quelle che si aspettavano rispetto alla distribuzione normale. Se la distribuzione di rendimento è inclinata verso la coda sinistra, l’asimmetria sarà negativa è indicherà che sono presenti deviazioni estreme di rendimenti negativi nella serie. L’asimmetria relativa di due strategie mostra la possibilità di maturare un grande rendimento ‘a sorpresa’ o una deviazione estrema. L’asimmetria è maggiormente influenzata da ogni deviazione estrema. Per esempio, l’asimmetria di rendimenti di una grande compagnia azionaria nel periodo tra Gennaio 1971 e Dicembre 2000 era di -0,36, ma escludendo la deviazione estrema i rendimenti di più di 3 deviazioni standard dalla media cambierà l’asimmetria a -0,02.
Kurtosis (Curtosi)
Una distribuzione non normale avrà anche molti o pochi rendimenti al centro della distribuzione rispetto ad una distribuzione normale.
Osservazione 29> La curtosi è il grado attraverso il quale l’istogramma di una serie di rendimenti sarà più appuntito o più piatto rispetto a quello descritto dalla distribuzione normale. Il grado di curtosi si può calcolare attraverso l’equazione:

Procedimento operativo (consiglio: c’è anche la built-in function in excell che calcola direttamente la curtosi)
- prendere la differenza tra i rendimenti mensili e il rendimento medio aritmetico.
- dividere la differenza per la deviazione standard dei rendimenti.
- sommare le differenze risultanti.
- dividere la somma delle differenze per il totale dei rendimenti.
La curtosi di una distribuzione di rendimento normale è uguale a 3. Per semplificare l’interpretazione della curtosi, spesso si riporta solo la curtosi in eccesso, la quale è uguale alla curtosi meno 3.
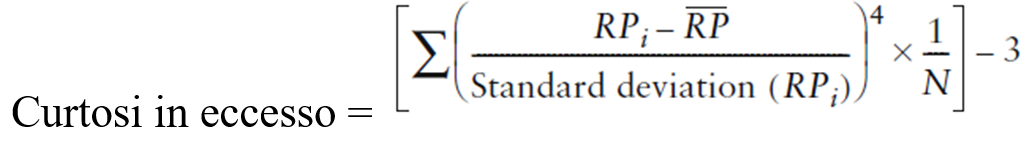
Come l’asimmetria, la curtosi non ha significato in termini di rendimenti; è solo una metrica della forma di una distribuzione dei rendimenti che, nel nostro esempio ha un eccesso di curtosi di -1,04 per il fondo e -1,59 per il benchmark. Lo schema Excell mostra il calcolo della curtosi in eccesso.
Esistono due tipo di curtosi:
- L’eccesso di curtosi positiva indica un picco maggiore del normale, o leptocurtosi, della distribuzione del rendimento. Una distribuzione con un picco maggiore ha più casi di rendimenti vicini alla media e rendimenti più positivi o negativi rispetto ad una distribuzione normale di rendimenti. Quindi l’eccesso di curtosi positiva indica una distribuzione con coda ‘più grassa’ rispetto al normale. La distribuzione ‘a coda grassa’ è rilevante in termini di volatilità perché indica che ci aspettiamo di vedere più frequentemente rendimenti estremamente alti o bassi rispetto a quella che indicherebbe la distribuzione normale.
- La curtosi in eccesso negativa indica invece un abbassamento rispetto normale ed è indicativa di una distribuzione cd platicurtica. È possibile vedere che la distribuzione di grandi compagnie azionarie è ‘a coda grassa’ guardando l’istogramma nello schema 9,2.
Test di verifica della distribuzione normale (o test di non normalità)
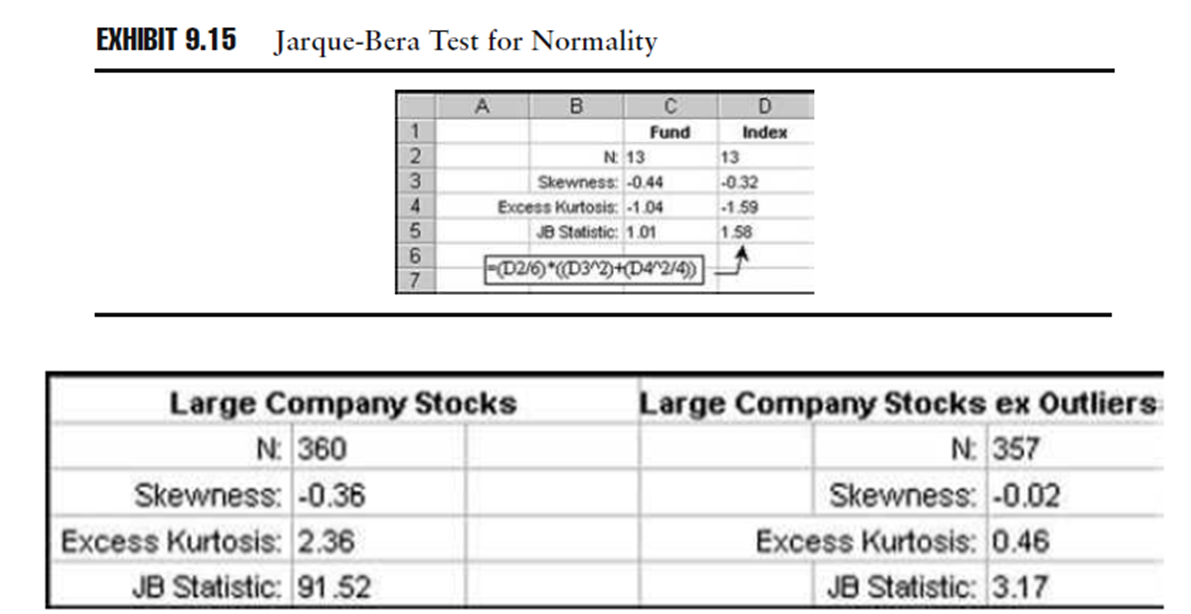
L’asimmetria e la curtosi insieme ci dicono se dobbiamo “sorprenderci” dei rendimenti estremi. Per esempio, un’asimmetria vicino a -1 insieme alla curtosi in eccesso maggiore di 1 mostra che abbiamo registrato rendimenti negativi più grandi di quelli che indicherebbe la deviazione standard. Quello che è importante è che, una volta presa la statistica dell’asimmetria insieme a quella della curtosi, si possa indicare se la distribuzione dei rendimenti sia normale o no. Il test Jarque-Bera (JB) può essere usato per questo scopo.
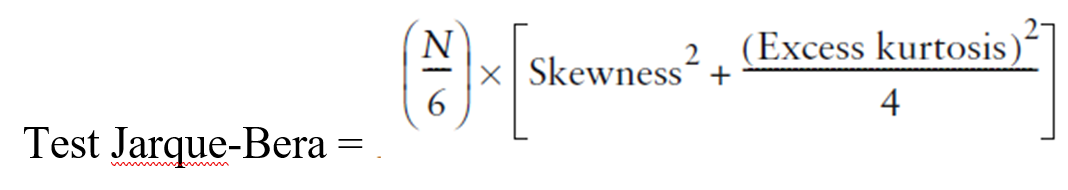 Il JB test confronta i valori dell’asimmetria e della curtosi con i valori aspettati se la distribuzione fosse normale. Il risultato del JB test maggiore di 6 (circa) su una grande serie di dati, indica che la distribuzione di rendimento potrebbe non essere distribuita normalmente. Il fondo del nostro esempio e l’indice hanno entrambi una statistica JB sotto al 6, ma “sfortunatamente” nel nostro esempio vengono usati solamente 13 fondi mensili e indici di rendimento, implicando con ciò che il JB test non è utile per piccoli numeri di osservazioni.
Il JB test confronta i valori dell’asimmetria e della curtosi con i valori aspettati se la distribuzione fosse normale. Il risultato del JB test maggiore di 6 (circa) su una grande serie di dati, indica che la distribuzione di rendimento potrebbe non essere distribuita normalmente. Il fondo del nostro esempio e l’indice hanno entrambi una statistica JB sotto al 6, ma “sfortunatamente” nel nostro esempio vengono usati solamente 13 fondi mensili e indici di rendimento, implicando con ciò che il JB test non è utile per piccoli numeri di osservazioni.
Possiamo, comunque, attuare il JB test sulla serie di rendimenti mensili delle azioni di società large cap dal 1971 al 2000. Il JB test risulta per questa asset class a 91,52, indicando che la distribuzione dei rendimenti si allontana dalla normalità. Lo stesso calcolo, escludendo i 3 rendimenti mensili che sono deviazioni estreme, corrisponde a 3,17.
Fonte: Investment Performance Measurement (Bruce J. Feibel)
Osservazione 30 > Presi insieme, la statistica dell’asimmetria e della curtosi indicano che dovremmo aspettarci più rendimenti estremi rispetto a quelli che indicherebbero le deviazioni standard. Possiamo confrontare queste statistiche per differenti investimenti per avere un’idea riguardo al rischio relativo associato agli eventi estremi.
rischio assoluto e distribuzione
Nel prossimo articolo la trattazione si spostera sulla misurazione del rischio a ribasso: Come misurare il rischio a ribasso (o Downside Risk) con Excel? Scopriamolo!
Come sempre, spero di non aver fatto figuracce nell’esplicazione dell’argomento trattato.
Yours best
DF
