Nel precedente articolo (Vedi: Come calcolare correttamente il rendimento di un fondo? Scopriamolo!) abbiamo analizzato come calcolare correttamente il rendimento di fondo comune d’investimento. In questo articolo invece si prosegue partendo dai rendimenti di un determinato periodo (settimane, mesi, anni, MTD, YTD, ecc) per concatenarli e determinare il rendimento multi periodo. Anche in tal caso, come sempre, occorre introdurre un po’ di matematica ma niente paura, in allegato troverai un Tool di Esempio in Excel che ti mostrerà come fare (il consiglio è tuttavia quello di imparare l’utilizzo di Excel per capire come effettuare rapidamente più operazioni).
Mi scuso in anticipo per la “rozzezza” delle equazioni presentate e della presentazione in Excel (spero non ci siano errori di calcolo) ma l’importante, come sempre, è rendere l’idea.
Rendimenti cumulativi
Il modus operandi di composizione del rendimento partendo dai rendimenti dei sottoperiodi (usando il TWR) è già stato spiegato.
Quando si concatenano più rendimenti per calcolare il rendimento di un lasso di tempo maggiore si determina il rendimento cumulativo. Alcuni esempi di lassi di tempo di rendimento cumulativo riguardano il MTD (month-to-date, ossia l’arco temporale compreso tra l’inizio del mese in corso e la data attuale), il YTD (year-to-date, ossia l’arco temporale compreso tra l’inizio dell’anno e la data attuale), il primo trimestre dell’anno, un anno, tre anni ecc.
Procedimento operativo
Passo 1 > converto ogni rendimento in un tasso di crescita (dato dalla somma fra 1 ed il rendimento, dove 1 è il capitale unitario di partenza e il rendimento è l’incremento/il decremento di valore del capitale)
Passo 2> moltiplico i tassi di crescita per determinare il rendimento cumulativo
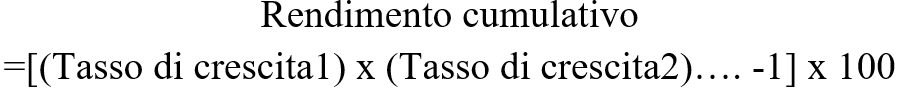
Per esempio, se: tasso di crescita1 = 1,12, tasso di crescita2 = 1,174
Rendimento cumulativo = [ (1,12 x 1,174) – 1 ] x 100 = 31,488%
Dove i tassi di crescita composti su più di un periodo vengono detti tassi di crescita cumulativi (se si dispone di un tasso di crescita cumulativo si può calcolare direttamente l’incremento di valore dell’investimento senza calcolare rendimenti o tassi di crescita dei vari sottoperiodi).
Valore finale = 100 € x 1,1865 = 118,65 €
In alternativa i tassi di crescita posso essere usati per calcolare il rendimento tra due date:

I rendimenti cumulativi vengono quindi determinati sostanzialmente quando si è interessati alle performance di investimenti a lungo periodo.
Osservazione 1: i rendimenti cumulativi si basano sull’ipotesi per cui i profitti degli investimenti vengono reinvestiti nel portafoglio e ricollegati nel tempo. L’incremento/decremento alla fine di ogni periodo, che viene misurato dal rendimento, viene pensato come se fosse un utile che viene reinvestito nel portafoglio nel periodo successivo (e quindi accumulato nel tempo)
Osservazione 2: i rendimenti dei singoli periodi vengono spesso determinati su base giornaliera o mensile. Questo tipo di rendimenti possono essere usati per essere “compressi” in rendimenti di più lungo termine mediante la procedura di composizione del rendimento.
In base all’osservazione 2, i rendimenti giornalieri calcolati nel lasso temporale di un mese possono essere usati per determinare il rendimento mensile. Collegare i rendimenti di 12 mesi determina lo stesso risultato come se i rendimenti giornalieri venissero composti nell’arco di un anno. Con tale approccio i rendimenti mensili possono essere compressi nei rendimenti annuali con lo scopo di calcolare i rendimenti multi annuali ecc. Nell’esempio in excell, si utilizzano 7 rendimenti con frequenza annuale per ricavare il rendimento cumulativo settennale. Se i rendimenti annuali venissero calcolati usando rendimenti con frequenza giornaliera, avremmo potuto comporli approssimativamente nei 1250 rendimenti (250 giorni di negoziazione x 5 anni) e ricavare lo stesso risultato. Talvolta è più facile lavorare con rendimenti compressi mensilmente, trimestralmente o annualmente, anche se poi sono originariamente calcolati giornalmente.
Rendimento medio aritmetico
Quando si vuole valutare il risultato di un investimento è prassi diffusa utilizzare la media dei rendimenti, che può essere usata per confrontare la performance dei diversi portfolio manager o dei fondi nel tempo.
Esistono due metodi per calcolare la media di una serie di rendimenti: il metodo aritmetico e il metodo geometrico.
La media aritmetica dei rendimento si calcola come la somma dei rendimenti periodici diviso per il numero dei rendimenti:
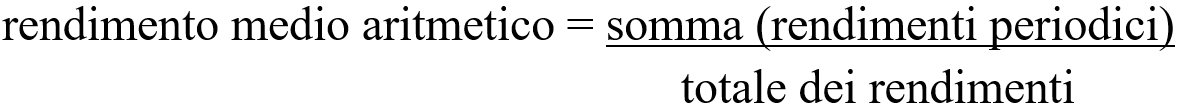
Osservazione 3: il lasso di tempo a cui i rendimenti si riferiscono deve essere lo stesso (giornaliero, settimanale, mensile, annuale ecc.)
Questo tipo di rendimento viene spesso utilizzato nella misurazione del rischio che il portafoglio ha sperimentato ma non può essere usato in tutte le applicazioni, come ad esempio nel proiettare il valore futuro di un investimento (dove ad esempio deve essere utilizzato il rendimento medio geometrico, che riconcilia valore iniziale e valore finale)-
Esempio di calcolo del rendimento medio aritmetico:
Anno 1: rendimento 5%
Anno 2: rendimento 3%
Anno 3: rendimento 8%
Rendimento medio aritmetico = [ ( 5% + 3% + 8% ) ] / 3 = 5,33%
Mentre il rendimento composto a 3 anni è:
Rendimento composto = [ ( 1,05 x 1,03 x 1,08 ) -1 ] = 16,802%
Osservazione 3: Se usiamo il rendimento medio aritmetico per inserirlo nella formula del rendimento composto, troveremo un risultato diverso da quello che avremmo ottenuto utilizzando i rendimenti periodici effettivi:
[ ( 1,0533 x 1,0533 x 1,0533 ) -1 ] = 16,857%
Usare il rendimento medio aritmetico per calcolare il valore futuro dell’investimento provoca una sopravvalutazione (il rendimento deve essere minore per considerare il processo di composizione fra vari periodi).
Rendimento medio geometrico
Quando si moltiplica la media del rendimento annuale per il numero totale degli anni, il risultato non sarà uguale al rendimento composto perché non tiene in considerazione gli interessi maturati sugli interessi (legge dell’interesse composto). Per effettuare il calcolo dell’interesse composto, invece della media aritmetica, si calcola la media geometrica del rendimento. Il rendimento medio geometrico è la radice ennesima del rendiconto composto, dove n è il numero dei periodi usati per calcolare il rendimento cumulativo (se N = 3 la radice di 3 è l’elevazione a potenza di 1/3)
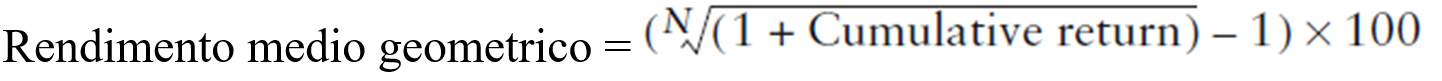
Nell’esempio precedente (dove ^ rappresenta l’elevazione a potenza (ossia l’inverso di N):
Rendimento medio geometrico = [ (1 + 16802)^(1/3) -1 ] x 100 = 5,31334966%
Inserendo il rendimento medio geometrico nella formula di crescita composta, si calcola il rendimento composto del periodo.
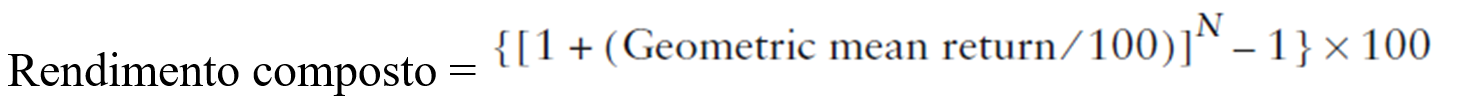
Avendo il rendimento medio geometrico al 5,3133496%, possiamo ricavare il 16,857% del rendimento composto di due mensilità.
{ [ 1 + ( 5,3133496 / 100 ) ] ^3-1 } x 100 = 16,802%
Osservazione 4: Mentre il rendimento medio aritmetico può essere aggiunto per ricavare la somma aritmetica dei rendimenti di un fondo, i tassi di crescita medi geometrici possono essere moltiplicati per calcolare il rendimento multi periodo composto. Poiché i rendimenti medi geometrici sono stati usati per essere composti e per rispecchiare la crescita delle disponibilità monetarie nel tempo, saranno sempre inferiori o uguali al rendimento medio aritmetico. La media geometrica sarà uguale solamente alle media aritmetica se e solo se la crescita rimane costante nel tempo.
Vedi Excell foglio 1
Usare i rendimenti calcolati nel tempo continuo
Per calcolare il rendimenti medio geometrico multi periodo si calcola il prodotto dei tassi di crescita dei singoli periodi e poi si applica la radice ennesima del risultato, dove n rappresenta il numero dei periodi. Un’alternativa a questo calcolo è l’uso dei rendimenti composti continui. Si fa questo prendendo la media aritmetica dei logaritmi naturali dei tassi di crescita e ponendo poi la base del logaritmo naturale e alla potenza del risultato.
Prendendo il logaritmo del tasso di crescita del singolo periodo, si potrà calcolare un rendimento composto continuo per ogni periodo (come se il denaro crescesse istante per istante nel tempo: da ciò il detto il denaro non dorme mai). Innalzando e alla media dei tassi di crescita composti continui si renderà il rendimento medio geometrico.
Esempio
partendo dai tassi di crescita precedenti per il calcolo del rendimento medio geometrico:
Media aritmetica dei logaritmi dei tassi di crescita = [ Ln(1,05) x Ln (1,03) x Ln (1,08) ] / 3 = 0,05177
e^(media) = 1,0531335
Rendimento medio geometrico = ( 1,0531335 – 1 ) x 100 = 5,31335%
(Vedi Excell foglio 1)
Rendimenti annualizzati
I rendimenti sono in genere espressi su base annuale. Ciò perché si facilita il raffronto trai rendimenti di investimento se il periodo di tempo è lo stesso per ogni investimento: non è possibile confrontare un rendimento cumulativo del 10% con un altro del 12% se il primo è stato maturato in 5 mesi e l’altro in 12 mesi. Per analizzare la differenza dei rendimenti tra i due investimenti, sarà utile mantenere il periodo costante. I rendimenti cumulativi calcolati usando i rendimenti di periodi superiori o inferiori ad un anno, possono essere espressi su base annuale. Il rendimento medio geometrico, quando viene calcolato per un periodo di 1 anno si chiama rendimento annualizzato, rendimento medio annuo o rendimento annuo composto. Computando i rendimenti su base annuale, si facilita il confronto tra i rendimenti di portafogli con diverse date d’inizio e di fine.
I tassi di interesse sono per convenzione quotati su base annuale. Se un investitore acquista uno strumento a reddito fisso con un periodo di maturazione di un mese e una frequenza di capitalizzazione mensile, il tasso quotato sarà il tasso annuale del 6% e non il tasso mensile di circa lo 0,487%.
Esempio
Tasso mensile = 0,5%
Tasso annuale = 6%
Rendimento mensile= [ (1,06) ^ (1/12) ] = 0,004867551 (o 0,4867751%)
[ (1 + rendimento mensile)^(12) ] -1 = 0,06 (o 6%)
Se abbiamo un rendimento di un periodo inferiore ad un anno e abbiamo bisogno di convertirlo in un rendimento annuale, possiamo capitalizzarlo innalzando il periodo del tasso di crescita alla potenza uguale al numero di periodi dell’anno:
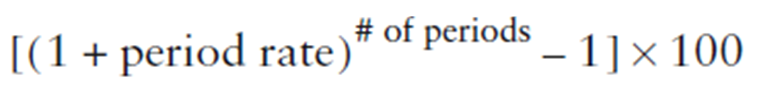
Osservazione 5: Occorrerebbe continuare a reinvestire ad ogni tasso del singolo periodo di approssimativamente lo 0,5% al mese per realizzare un rendimento annuale del 6%. Il problema principale nel quotare i tassi d’interesse e i rendimenti annualizzati su una frequenza inferiore ad un anno è che sono proiezioni ipotetiche del rendimento annuale, visto che non c’è garanzia che l’investitore sia capace di reinvestire allo 0,5% al mese per realizzare il 6% di rendimento annuale.
Come esempio estremo del problema dell’utilizzo dei rendimenti annuali creati in questo modo, supponiamo che il mercato abbia un mese proficuo superiore al 30%. La conversione su base annuale porta ad un rendimento annuale composto del 1099%.
[ ( 1 + 0,25) ^12 -1 ] x 100 = 1099,11638%
Osservazione 6: Molte volte non si annualizza fino a che una serie di rendimenti periodici non contengano un anno di osservazione.
Se il rendimento del periodo è maggiore di un anno, il tasso è usualmente ripetuto in base annuale usando la formula di capitalizzazione inversa a quella usata sopra. Prendere specularmente un numero ed elevarlo alla potenza n-esima per avere la radice ennesima del numero:
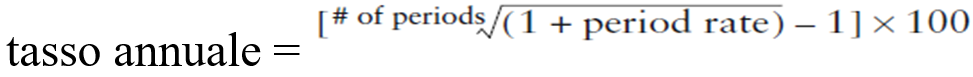
Un rendimento del 12,4864% a 3 anni corrisponde ad un rendimento del 4% ad 1 anno
[ 1,124864 ^ (1/3) -1 ] x 100 = 4%
Osservazione 6: si sta calcolando il rendimento annualizzato prendendo prima la radice ennesima di un tasso di crescita cumulativo, o 1,124864 come nel nostro esempio, invece di prendere la radice ennesima del rendimento cumulativo. La radice ennesima del tasso di crescita è il tasso di crescita medio geometrico. Per convertirlo in un rendimento medio geometrico basta sottrarre 1 e moltiplicarlo per 100 (per esprimerlo in %). La media annuale di un rendimento composto al 12,4864% in tre anni è il 4%.
Quando si vuole calcolare un rendimento annualizzato per periodi cumulativi che non sono esattamente multipli di un anno, si deve contare l’esatto numero di giorni del periodo cumulativo e dividerlo per 365.25 per calcolare l’equivalente annuo (dato che è la radice, se si vuole elevare a potenza occorre dividere 365,25 per il numero di giorni):
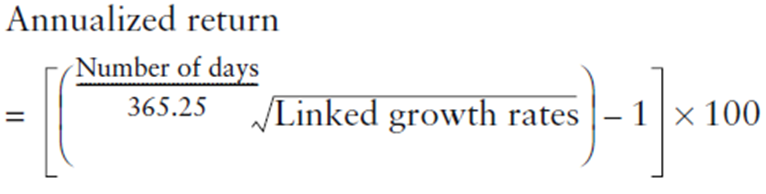
Suggerimento: se non si vogliono usare built-in function di Excel per calcolare il numero di giorni fra due date usare il sito http://calendario.eugeniosongia.com/duration.htm.
Es > se il periodo va dal 31/12/1998 al 31/05/2000 i giorni sono 517. Se il rendimento del periodo è del 15% il rendimento annualizzato a 17 mesi è di:
Rendimento annualizzato di 17 mesi = [ (1,15) ^ (365,25/517) – 1 ] x 100 = 10,37781469%
Il modus operandi più diffuso per il calcolo di periodi superiori ad un anno è di presentare il rendimento medio annuale usando la media geometrica. Per esempio, un 15.00% di rendimento medio geometrico basato su un rendimento composto in 2 anni, viene presentato come un “rendimento annuale medio di 2 anni”. La presentazione della performance del fondo include normalmente un rendimento di media annuale di diversi periodi maggiori di un anno: 3 anni, 5 anni, 10 anni, la contabilità dall’inizio e così via, dove ogni rendimento viene espresso su base annuale.
Osservazione 7: se c’è variabilità nei rendimenti periodici, il rendimento medio geometrico sarà sempre inferiore al rendimento medio aritmetico. La media aritmetica tratta in egual modo i rendimenti positivi e negativi. Per esempio, un rendimento positivo del 50% e uno negativo del 50% si compensano a vicenda usando un media aritmetica:
( 0,5 – 0,5 ) / 2 = 0
In realtà, una crescita positiva del 50% nel periodo 1 seguito da una decrescita del 50% nel periodo 2 causano una decrescita del valore dell’investimento nei 2 periodi. Per esempio, se partiamo con $100, un rendimento positivo del 50% e poi negativo del 50% causeranno un valore finale di $75.
100 € x ( 1+ 0,5 ) x ( 1 – 0,5 ) = 75 €
Tasso Interno di Rendimento composto
Il TWR è la misurazione “corretta” per determinare il rendimento del manager quando questo non ha potere discrezionale sulla tempistica e l’ampiezza dei flussi di cassa. Se il manager ha il controllo sui flussi di cassa, allora il MWR è la misurazione più adatta del rendimento per rispetto al TWR per quanto riguarda le performance del manager. Per esempio, i fondi di private equity utilizzano le risorse degli investitori gestendole a monte ed investendole -nel lungo termine- in titoli non negoziabili emessi dalle compagnie. Questi includono capitale di rischio e altri tipi di investimenti privati.
Alla fine il manager restituisce il denaro agli investitori visto che hanno venduto le quote. Inoltre, per gestire questi flussi di cassa, il MWR fornisce anche una buona soluzione nel calcolare i rendimenti di portafoglio, in cui i valori degli investimenti nelle date dei flussi di cassa non sono facili da individuare (ed è proprio l’esempio di un fondo di private equity). Per tenere in considerazione la tempistica di questi flussi di cassa e aggirare il problema di valutare la “non liquidità”, viene utilizzato l’IRR (Internal Rate Of Return o TIR, Tasso Interno di Rendimento) per calcolare il rendimento di ogni portafoglio.
Possiamo capitalizzare un IRR equivalente annuale per periodi superiori ad un anno. Perciò tutto quello che bisogna fare è rettificare i flussi di cassa stimati così che risulteranno multipli di un anno. (Vedi Excell foglio 1)
Analisi del rendimento multi periodo
Osservazione7: l’esempio multi periodo evidenzia la differenza tra il MWR e il TWR sull’influenza dei flussi di cassa in una performance. Anche se si calcola il TWR per valutare la performance di un portfolio manager, il MWR è ancora importante nella misurazione della crescitadi valore nel tempo degli asset del fondo. Se non ci sono flussi di cassa durante il periodo, il TWR e il MWR sono uguali. Quando ci sono flussi di cassa, invece, il TWR e il MWR saranno diversi perché il MWR considera i flussi di cassa mentre il TWR no.
Si dimostrano queste affermazioni con un esempio in cui il manager è responsabile della gestione dei due portafogli utilizzando la stessa strategia e tutti e due i fondi abbiano lo stesso rendimento. I clienti A e B guadagnano in 5 anni gli stessi rendimenti annuali. Il cliente A non ha flussi di cassa all’investimento iniziale di $1000.
Calcolo del MWR del cliente A: visto che non ci sono flussi di cassa, il MWR e il TWR del cliente A sono uguali. Il modello del flusso di cassa del cliente B si differenzia nel fatto che lui ha fatto un investimento iniziale di $200 e investimenti successivi di $200 all’inizio dei successivi 4 anni. Visto che il cliente B ha più denaro in azione nei periodi in cui i rendimenti erano alti, il suo MWR è maggiore rispetto a quello del cliente A. Nello schema excell il calcolo dell’IRR del cliente B. il MWR annualizzato è di 2.56%, significativamente maggiore rispetto al TWR annualizzato che è uguale a -0.16%.
La sequenza del rendimento influenza il MWR ma non il TWR
Lo schema Excell mostra anche un’altra proprietà interessante dei rendimenti multi periodo. L’ordine dei rendimenti, senza considerare quando calcoliamo il TWR, influenza il MWR quando ci sono i flussi di cassa. Questo perché il MWR è un tasso di interesse singolo che collega il valore iniziale e finale di un investimento, data la sequenza dei flussi di cassa. Nello schema Excell possiamo vedere che i clienti C e D ottengono gli stessi rendimenti annuali dei clienti A e B, eccetto per il fatto che l’ordine degli investimenti sia opposto.
Invece di maturare rendimenti negativi nei primi anni, il manager matura rendimenti positivi e viceversa. Poiché non ci sono flussi di cassa, il MWR dei clienti A e C sono uguali al TWR. Dato che l’ordine dei rendimenti non impatta quando si calcola il TWR (i TWR sono commutativi), i TWR dei clienti A e C sono uguali. Ma il MWR è influenzato dall’ordine dei rendimenti quando sono presenti flussi di cassa. È da notare che il MWR del cliente D, il quale ha lo stesso modello di flussi di cassa del cliente B, è significativamente inferiore al MWR del cliente B. Questo perché il cliente D aveva più denaro investito negli anni quando i rendimenti erano negativi. Lo schema excell mostrano il calcolo dell’IRR dei clienti B e D. (Foglio 3)
Osservazione 8: per calcolare l’IRR si veda questo video (e si consiglia di imparare l’uso di Excell)
Algoritmo di calcolo (Excell 2016):
passo 1> sul menu in alto c’è la sezione dati: cliccarci sopra
passo 2> cliccare analisi di simulazione
passo 3 > cliccare su riceva obiettivo
passo 3 > imposta il valore obiettivo differenza a 0
passo 4> modificando il valore del TIR annuale
passo 5> calcolare i valori futuri usando il TIR annuale
Nel prossimo articolo spiegheremo: Come analizzare il “rischio assoluto” e la distribuzione dei rendimenti tramite Excel? Scopriamolo!
Nota Bene: il trading e l’attività d’investimento in generale possono comportare rischi significativi per il capitale, con perdite che potrebbero in alcuni casi eccedere il capitale iniziale. Gli scenari di mercato cambiano continuamente e le performance passate non rappresentano garanzia delle performance future. È pertanto fondamentale assicurarsi di aver compreso tali rischi. Le informazioni presentate in questo sito non sono in alcun modo da intendersi come sollecito all’investimento e sono rivolte ad un pubblico indistinto, non rappresentando in alcun modo attività di consulenza finanziaria -e nemmeno generica- in base ai profili di rischio e rendimento degli investitori. Ogni decisione di investimento è sotto la piena ed esclusiva responsabilità del lettore. Né l’autore né InvestireOggi saranno responsabili nei confronti di nessun utente né di qualsivoglia altra persona o entità per l’inesattezza delle informazioni o per qualsiasi errore od omissione nei suoi contenuti, a prescindere della causa di tali inesattezze, errori od omissioni.
