Absolute Risk Adjusted Return. Cosa è e come calcolarlo. Scopriamolo!

La deviazione standard e le misure del rischio al ribasso quantificano la dispersione dei rendimenti ottenuti nel tempo e rappresentano i primi surrogati del rischio assoluto, mentre il Beta e ed il tracking risk (vedi il precedente articolo: Il rischio relativo. Cosa è e come misurarlo tramite excel. Scopriamolo!) ci forniscono misure del rischio relativamente al benchmark o generalemente asset.

Come in ogni argomento trattato il tutto sarà accompagnato da un foglio Excel che mostra i calcoli da effettuare (in modi diversi, sia tramite algoritmi di calcolo che mediante built-in function che facilitano il lavoro: nel foglio 1 coefficiente di variazione, Sharpe Ratio e Rendimento M quadro; nel foglio 2 il CAPM)

Osservazione 1 > Data una metrica del rischio, il prossimo obiettivo è di indirizzare l’argomento sul se il rendimento sia sufficiente, tenuto conto dei rischi assunti. Un modo per fare ciò è confrontare il rischio e i rendimenti maturati da una serie di portafogli di gruppi di pari e il nostro portafoglio con il benchmark: è possibile effettuare un confronto visuale creando un grafico in cui siano tracciate le combinazioni delle osservazioni rischio/rendimento di ogni portafoglio.

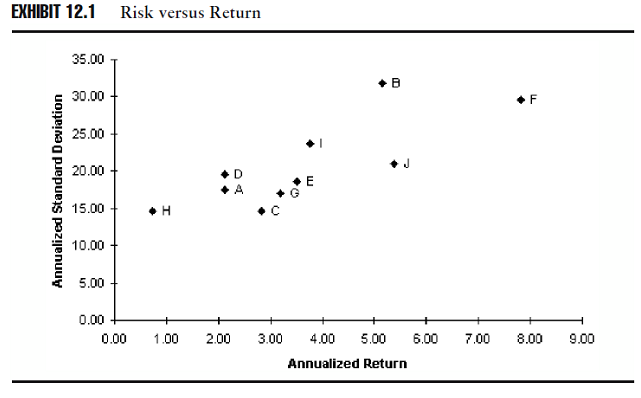
Lo schema 12.1 mostra 3 anni di un rendimento annualizzato e 3 anni di deviazioni standard di fondi di 10 grandi compagnie azionarie.

Fonte: Investment Performance Measurement (Bruce J. Feibel)

L’asse delle Y rappresenta la deviazione standard dei rendimenti nel periodo; l’asse delle X rappresenta le misure dei rendimenti, in questi caso il rendimento medio aritmetico, del periodo. È possibile vedere che c’è un relazione generale tra i rischi presi e i rendimenti maturati. Ma ci sono anche alcune eccezioni: il fondo B mostra la deviazione standard più alta, ma matura un rendimento più basso rispetto ai fondi F e J. I fondi C e H hanno approssimativamente lo stesso rischio, ma i fondi F hanno un rendimento più alto.

Quindi è importante relazionare il rischio e il rendimento per valutare la performance di un fondo.

Oltre alla rappresentazione grafica, sarebbe fruttuoso avere misure numeriche dei rischi e rendimenti congiunti mostrati dal portafoglio.

Osservazione 2> È possibile rettificare i rendimenti maturati nel tempo con la deviazione standard del rendimento e altre descrizioni statistiche dei rischi presi allo scopo di ricavare misure di rendimenti rettificati per il rischio. I rendimenti rettificati per il rischio (o risk-adjusted) sono misure di rendimenti e rischi compositi che sono usati per aiutare a determinare se i rendimenti maturati sono o no sufficienti in confronto a quelli maturati da portafogli e benchmark simili che mostrano un simile livello di rischio. Esistono differenti modi per determinare i rendimenti rettificati per il rischio di un portafoglio. In questo capitolo considereremo le misure del rendimento rettificato per il rischio calcolato in un contesto del Modern Portfolio Theory (MPT). Le statistiche basate sul MPT valutano il rischio usando il Capital Asset Pricing Model (CAPM), un modello teorico del rischio e del rendimento.

Coefficiente di variazione

Osservazione 3> Data la deviazione standard come una misura della variabilità di un rendimento, è naturale voler confrontare due investimenti per determinare se uno è più instabile dell’altro.

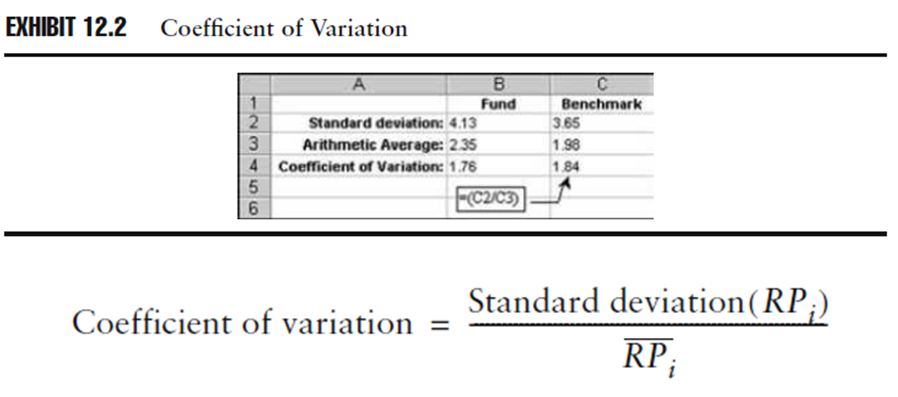
Possiamo vedere negli esempi precedenti che il fondo di riferimento ha una deviazione standard del rendimento nel periodo più alta del benchmark, 4,13% e rispettivamente 3,65%. Comunque, la media aritmetica del rendimenti di fondo è anche più alta rispetto alla media aritmetica del rendimento del benchmark del periodo.

Osservazione 4> Visto che la deviazione standard viene calcolata nelle stesse unità del rendimento come il rendimento medio- la deviazione standard dei rendimenti di investimenti differenti non è direttamente comparabile, a meno che le medie non siano simili. Per confrontare due investimenti in base alla loro variabilità relativa abbiamo bisogno di normalizzare la deviazione standard. Il coefficiente di variazione è una misura del rendimento rettificato per il rischio (risk-adjusted). È uguale alla deviazione standard ridimensionata in base alla media della serie storica dei rendimenti.

Il coefficiente di variazione è espresso come una rapporto: può essere usato per confrontare la variabilità relativa di due serie di dati, in tal caso la variabilità dei rendimenti di due fondi

Lo schema 12.2 mostra il calcolo dei coefficienti di variazione del nostro fondo e benchmark di riferimento.

Fonte: Investment Performance Measurement (Bruce J. Feibel)

Osservazione 5> Le deviazioni standard sono approssimativamente 1,76 volte la media del fondo del rendimento e 1,81 volte della media del benchmark. Da ciò si evince che la variabilità dei rendimenti del benchmark, espressi come la percentuale della media di rendimento, è maggiore rispetto alla variabilità dei rendimenti del fondo; questa è la conclusione opposta a cui si arriva confrontando le deviazioni standard assolute.

Indice di Sharpe (o Sharpe Ratio)

Osservazione 6> I rapporti si usano per fare confronti tra due variabili: un rapporto in sé è parametro di confronto in situazioni in cui esistono differenze nelle misure assolute che vengono comparate. Per esempio, io posso fare un viaggio breve e tu un viaggio lungo, ma se si è interessati in chi guida più veloce lungo il percorso, possiamo normalizzare le distanze e i tempi comparando la media di velocità considerata in chilometri all’ora.

Osservazione 7> Analogamente, se siamo interessati a confrontare il rischio all’efficienza del rendimento delle due strategie, possiamo prendere l’inverso del coefficiente della determinazione dividendo la media di rendimento del periodo per il rischio preso durante il periodo per ricavare il rendimento per unità di rischio. Questa misura è spesso chiamata rendimento rettificato per il rischio, o Risk-Adjusted Return.

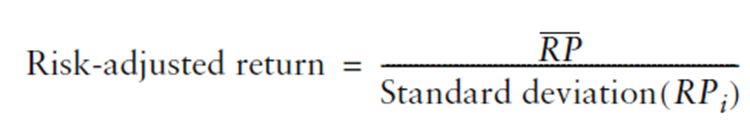
Fonte: Investment Performance Measurement (Bruce J. Feibel)

dove RPi sono i rendimenti periodici del fondo e RP soprasegnato è la media artimetica relativa. Il rendimento rettificato al rischio è equivalente all’inverso del coefficiente di variazione. Può essere usato per classificare l’efficienza dei rischi e dei rendimenti dei portafogli, ma non è spesso riportato.

Ossercazione 8> Il dr. William Sharpe, vincitore del premio Nobel e uno dei fondatori del Capital Asset Pricing Model, a cui è stato attribuito con lo sviluppo dell’indice di Sharpe per la misurazione della performance rettificata per il rischio. La rettifica -o aggiustamento- è basata sull’idea che non possiamo guadagnare rendimenti nel tempo, al di sopra dei rendimenti non rischiosi e senza assumere alcun rischio. Il rendimento non rischioso è un rendimento che possiamo maturare su un investimento con un piccolo o senza mercato o rischio di credito, come un T-bill americano. È il rendimento su un rendimento non rischioso che ci si aspetterebbe di maturare sopportando il mercato e il rischio di credito che accompagna molti investimenti. Questo rendimento viene chiamato extra-rendimento, equivalente alla differenza tra il rendimento periodico maturato su un investimento e il tasso non rischioso (risk-free; anche se oggi vale anche la legge dei tassi negativi per i rendimenti chiamati convenzionalmente risk free)) del periodo.

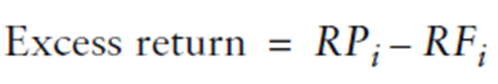
Fonte: Investment Performance Measurement (Bruce J. Feibel)

dove RFi sono i rendimenti periodici dell’investimento non rischioso.

Osservazione 8> Data la deviazione standard come deputata del rischio, teoricamente non ci dovrebbero essere deviazioni standard dei rendimenti per investimenti non rischiosi. Quindi è l’extra-rendimento che matura in cambio di assumere un certo grado di rischio. L’indice di Sharpe prende in considerazione questi costrutti teorici relazionando l’extra-rendimento del fondo al rischio, invece di usare il rendimento assoluto del fondo.

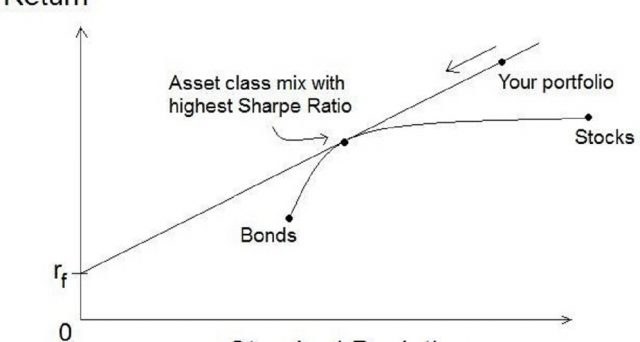
Osservazione 9> La Capital Market Line si riferisce alle proprietà del rischio e del rendimento dei vari investimenti. L’intercetta sull’asse del rendimento del CML è uguale alla media del tasso non rischioso.

L’indice di Sharpe può essere visualizzato come la pendenza (slope) della linea relativa ai modelli teorici del rischio e del rendimento, come il Capital Market Line nello schema 12.3.

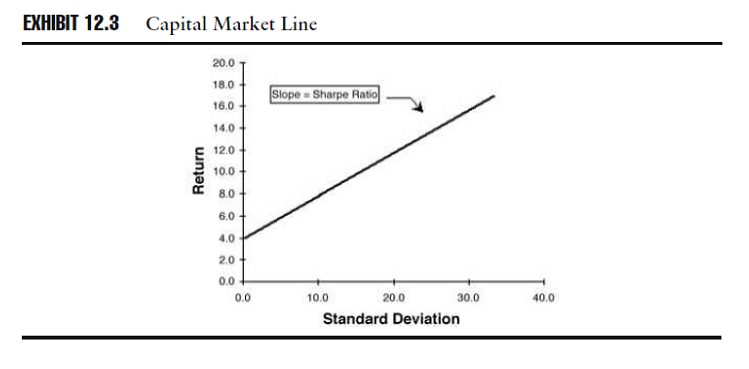
Fonte: Investment Performance Measurement (Bruce J. Feibel)

L’indice di Sharpe è la differenza tra il rendimento medio aritmetico annuale del fondo e il rendimento medio aritmetico non rischioso diviso per la deviazione standard annualizzata del rendimento del fondo.

Fonte: Investment Performance Measurement (Bruce J. Feibel)

Il Dr. Sharpe chiama tale indice rapporto guadagno-rischio (reward to risk ratio).

Procedimento operativo:

Sottraggo alla media annuale dei rendimenti periodici del fondo la media annuale dei rendimenti non rischiosi per formare il numeratore.
In seguito divideremo la differenza tra le medie per la deviazione standard annualizzata dei rendimenti del fondo per produrre l’indice rendimento/rischio

Osservazione 10> Possiamo anche calcolare gli indici di Sharpe e gli altri rendimenti rettificati per il rischio usando i rendimenti geometrici. Per fare ciò calcoleremo la differenza tra il rendimento geometrico di fondo e il rendimento geometrico non rischioso, e la divideremo per la deviazione standard del logaritmo naturale dei tassi di crescita dei singoli periodi. Spesso, operativamente, alcuni professionisti mischiano le strategie geometriche e aritmetiche, usando il rendimento medio geometrico a numeratore e la deviazione standard dei rendimenti periodici attorno al rendimento medio aritmetico a denominatore.

La differenza tra l’indice di Sharpe e il rendimento rettificato per il rischio è quella di sottrarre il tasso non rischioso dal rendimento “lordo” quando si calcola l’indice di Sharpe. Ciò ha l’effetto di rimuovere la porzione di rendimento prodotta dal tasso non rischioso, per il quale non ci si aspetta di subire “alcun rischio” (anche se dopo il 2008 anche i tassi convenzionalmente definiti risk free sono diventati rischiosi in realtà).

L’indice di Sharpe del nostro fondo di rendimento, calcolato nel foglio Excel, è uguale a 1,62.

Osservazione 11 > L’indice di Sharpe rivela l’efficienza del rapporto rischio/rendimento (o alternativamente il premio di rendimento in eccesso per ogni unità di rischio assunto) di un portafoglio. È possibile comparare gli investimenti con simili caratteristiche di rischio con l’indice di Sharpe per identificare il portafoglio più efficiente fra le varie alternative. Usando l’indice di Sharpe, possiamo mettere in pratica l’idea che non è possibile confrontare solo i rendimenti assoluti maturati su un investimento, ma anche tenere a mente la partecipazione al rischio che si sta correndo.

Due manager con rendimenti simili si possono differenziare in “modalità” rettificata per il rischio usando l’indice di Sharpe. Più l’indice di Sharpe è alto, più il rendimento del fondo è elevato per unità di rischio. La media degli indici di Sharpe differirà a seconda del tipo di portafoglio e del periodo di tempo usato, ergo è difficile offrire un idea di cosa sia un ‘buon’ indice di Sharpe senza guardare quello relativo ad altri fondi. Un indice di Sharpe negativo indica che il fondo ha avuto una scarsa performance rispetto all’investimento non rischioso. Non possiamo comunque usare solo gli indici di Sharpe per selezionare gli investimenti: come esempio da prendere in considerazione, un fondo con rendimenti bassi e deviazioni standard basse potrà esibire un indice di Sharpe maggiore rispetto al fondo con rendimenti assoluti più elevati e richiesti dallo scenario d’investimento.

Rendimenti non rischiosi

Osservazione 12> Il rendimento di un investimento non rischioso si utilizza computare l’indice di Sharpe e le altre statistiche del Capital Asset Pricing Model. Il tasso non rischioso è un tasso soglia, o anche detto benchmark del rischio. Un investimento non rischioso è un investimento in cui il rendimento effettivo corrisponde al rendimento atteso, ossia quando “teoricamente” non c’è varianza attorno al rendimento atteso (varianza pari a zero). In pratica, si usano i tassi sui titoli di Stato a breve termine per rappresentare l’investimento non rischioso perché essi non subiscono il rischio di credito (nb: dopo il 2008 sono considerati anch’essi rischiosi nella pratica, perché non esiste un investimento a varianza 0, anche i prezzi del titolo variano durante la vita dello strumento). Il rendimento su un investimento non rischioso rappresenta il puro valore temporale del denaro (che ora è diventato negativo: si pagà, cioè per prestare denaro); tutti gli altri investimenti che incorrono altri rischi, come ad esempio il rischio di default o il rischio di perdita del capitale, dovrebbero corrispondere un extra rendimento (o rendimento in eccesso) rispetto al tasso non rischioso.

Per selezionare il tasso non rischioso si sceglie convenzionalmente uno strumento con un tempo di scadenza che non abbia un rischio di reinvestimento: si utilizza il rendimento di T-bill di 30 giorni per effettuare un confronto con i rendimenti mensili di titoli rischiosi o di fondi. Visto che frequentemente si misura il rischio usando osservazioni trimestrali piuttosto che mensili, si userà un rendimento T-bill di 90 giorni se i rendimenti periodici saranno trimestrali invece che mensili. Il tasso non rischioso dovrebbe anche essere selezionato basandosi sulla valuta del portafoglio; in altre parole il tasso dell’euro dei fondi denominati in euro ecc.

Rendimenti M^2 (M-Squared Return)

Osservazione 13> Molti investitori tendono ad interpretare il significato economico trasmesso dal tasso di rendimento. Gli investitori professionisti comprendono le informazioni trasmesse dall’indice di Sharpe, ma molti utilizzatori delle statistiche di misurazione della performance che non lavorano giorno dopo giorno con questi strumenti trovano gli indici Sharpe fuorvianti perché non né conoscono gli input ed i significati.

Se un investitore non conosce quali fattori sono coinvolti, è difficile sapere se un fondo sia migliore perché non si ha un indice uguale, minore o maggiore.

Osservazione 14> Dato che il trade off (che possiamo considerare come una bilancia) del rischio/rendimento è il fulcro riguardo alla presa delle decisioni di un investimento in condizioni d’incertezza, lo sviluppo di una misura di performance aggiustata per il rischio non fuorviante e comprensibile da un vasto pubblico è di critica importanza.

Senza alcun tipo di misura, molti investitori potrebbero prendere decisioni basandosi sui rendimenti assoluti o con solo una considerazione approssimativa dei rischi presi per ottenere questi rendimenti; i regolatori e le industrie stanno ancora cercando questa misura.

Osservazione 14> Non esiste una statistica standard della performance rettificata per il rischio che abbia un supporto di base ampio come il TWR ha sulla misurazione della performance del rendimento, ma un candidato è il rendimento Modigliani e Modigliani, o rendimento M^2 (M al quadrato). Al dr. Franco Modigliani, Nobel per l’economia e persona insigne al MIT, e Leah Modigliani, analista a Morgan Stanley, viene attribuito lo sviluppo del rendimento M al quadrato per aiutare gli investitori confrontando i rendimenti che sono stati rettificati per il rischio (Franco Modigliani e Leah Modigliani, 1997).

Osservazione 15> Con M al quadrato si fa leva sul rendimento del fondo su o giù in base al rischio assunto; facciamo questo per mettere il fondo e il benchmark sulla stessa base di rischio prima di confrontare i rendimenti. Dato che è un rendimento, ha il beneficio di essere facile da comprendere. Per paragonare l’efficienza del rischio e del rendimento dei fondi, è possibile classificarli grazie a M al quadrato allo stesso modo con cui li classificheremo con l’indice di Sharpe.

M al quadrato è quindi l’indice di Sharpe ricalcolato considerando la deviazione standard del rendimento del benchmark.

Procedimento operativo:

calcolare l’indice di Sharpe per il periodo
calcolare poi la deviazione standard annualizzata dei rendimenti benchmark del periodo.
moltiplicare l’indice Sharpe per la deviazione standard annualizzata dei rendimenti del benchmark
aggiungere la media del rendimento annuale risk free

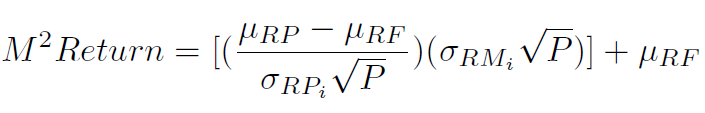
Fonte: Equazione di mia scrittura su LYX

Dove: la strana Mrp (mi) e Mrf rappresentano i rendimenti medi annualizzati rispettivamente del fondo e del titolo non rischioso; lo strano 6rpi (sigma) e 6rmi rappresentano le deviazioni standard (o volatilità) rispettivamente dei rendimenti del fondo e del mercato benchmark; P rappresenta il numero di periodi per annualizzare la deviazione standard (12 se i rendimenti sono mensili, 4 se sono trimestrali, 3 se sono quadrimestrali).

Il foglio Excell mostra il calcolo di M al quadrato del nostro fondo di riferimento, che corrisponde al 25,51%. È stato inoltre calcolato M al quadrato del benchmark, che corrisponde al rendimento benchmark del 23,81%.

Usando M al quadrato è possibile constatare che il fondo ha un rendimento maggiore rispetto al benchmark, anche se su base rettificata per il rischio. Possiamo confrontare il rendimento M al quadrato del fondo al rendimento del benchmark: Se M al quadrato è maggiore rispetto al benchmark, il fondo avrà un rendimento rettificato per il rischio positivo.

Osservazione 16> E’ possibile anche confrontare e classificare i fondi utilizzando il rendimento M al quadrato come se ogni rendimento del fondo fosse stato rettificato per avere la stessa instabilità del rendimento del benchmark; la classificazione relativa sarà la stessa di quella dei fondi fatta tramite l’indice di Sharpe, ma i risultati sono più facili da interpretare essendo espressi in termini di rendimento.

Capital Asset Pricing Model (CAPM)

Osservazione 17> L’analisi di regressione lineare è utilizzata in uno dei modelli più frequentemente usati nella definizione della relazione tra il rischio e il rendimento d’investimento, il Capital Asset Pricing Model, o CAPM. Sebbene originariamente implementato per spiegare la differenza fra i rendimenti prodotti dagli investimenti nelle singole azioni, il CAPM è stato per operativamente utilizzato per la valutazione della performancerisk adjusted del fondo d’investimento. Il CAPM è uno dei mattoni fondamentali della Moderna Teoria del Portafoglio, o MPT (Modern Portfolio Theory). I coefficienti di regressione che si ricavano usando il CAPM sono spesso chiamati statistiche MPT.

Il CAPM ha a che fare con la spiegazione delle differenze nei rendimenti maturati su diversi investimenti. Un investimento può essere composto da un singolo titolo o azione, o ancora un insieme di titoli di un fondo/portafoglio.

Usando un fondo d’investimento come nel nostro esempio, l’equazione del CAPM dipende da diversi principi:

Un investimento “senza rischi” maturerà il rendimento non rischioso, in cui il rischio viene misurato dalla volatilità dei rendimenti.
Due tipi diversi di rischio causano la volatilità nei rendimenti degli investimenti. Il primo è il rischio di mercato dell’investimento, che riflette il grado secondo cui gli investimenti variano quando il livello di prezzi nei cambiamenti di mercato evidenziati. La volatilità che impatta il mercato nel suo insieme si presume che corrisponda ai cambiamenti nei fattori evidenziati che influenzano i prezzi di mercato in generale. Come caso esplicativo, se ipotizzassimo che le valutazioni del mercato azionario rispondano positivamente agli incrementi nel tasso di crescita dell’economia nel suo insieme, possiamo affermare che il fattore di crescita economica è di qualche grado comune a tutte le azioni. La crescita economica e altri fattori che influenzano il valore dei prezzi di mercato interattivamente sono fattori di rischio sistematici.
I fattori di rischio sistematici sono riflessi nei rendimenti di mercato, perciò è possibile isolare la loro influenza sui titoli individuali osservando i rendimenti di mercato.
Tutti gli investimenti all’interno del mercato sono influenzati dal rischio sistematico, ma il grado di esposizione al rischio sistematico varia da titolo a titolo.
I fattori specifici dei titoli possono generare volatilità, per esempio, un cambiamento della gestione all’interno della compagnia. Questo tipo di volatilità è unica al titolo, o non sistematico (specifico, o idiosincratico).
Delle due componenti del rischio, quel rischio specifico a particolari titoli può essere eliminato attraverso la diversificazione di portafoglio. Ipotizziamo che i rischi particolari di diversi titoli si controbilanceranno nei rendimenti di fondi adeguatamente diversificati.
Data che il rischio totale è diversificabile, il mercato non ricompenserà il titolo con un premio per il rischio. Questo perché il rischio sistematico non può essere diversificato separatamente a costo zero ed è supportato da ogni investitore nel mercato.
Gli investitori si aspettano un premio per il rischio in cambio dell’assunzione del rischio.
Agli investimenti sono conferiti un grado di rendimento superiore al tasso non rischioso, o premio per il rischio, basato sul grado del rischio di mercato. Il rapporto guadagno/rischio (reward/risk ratio) è una funzione lineare, tale per cui per ogni unità di rischio sistematico a cui il titolo è esposto rispetto al mercato, il mercato stesso conferirà al titolo con un’unità di extra-rendimento.
Un investimento che ha esposizioni al rischio simile al mercato inteso nella sua interezza, avrà rendimenti che varieranno in linea con il mercato. Se un titolo è meno esposto ai fattori di mercato, i suoi rendimenti varieranno con un grado inferiore rispetto al mercato nel suo insieme. Se l’investimento ha una maggiore esposizione ai fattori sistematici, i rendimenti varieranno con un grado maggiore rispetto ai rendimenti di mercato.

Supponendo che queste affermazioni siano vere, la performance relativa da un titolo all’altro è determinata dal grado si rischio di mercato intrinseco nei due strumenti.

Osservazione 18> Possiamo formulare l’equazione di regressione rappresentante i principi del CAPM per ricavare il rendimento che dovremmo teoricamente osservare in un fondo dati i rendimenti di mercato, come rappresentato dall’indice di mercato o da altri benchmark.

Procedimento operativo>

1. ipotizziamo di avere un titolo privo di rischio di mercato. CAPM propone che un titolo privo si rischio di mercato maturerà un rendimento uguale al rendimento non rischioso, o:

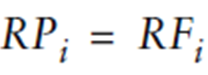
Fonte: Investment Performance Measurement (Bruce J. Feibel)

2.Se un titolo non è influenzato dagli elementi del rischio di mercato il CAPM afferma che dovremo ottenere un premio per il rischio proporzionato alla quantità di rischio di mercato riflesso nel titolo. Se il mercato sottostante stesso ha un grado di incertezza nel rendimento, si afferma che il rendimento di mercato sarà maggiore rispetto al rendimento non rischioso. Questo è un eccesso di rendimento di mercato.

Per ricavare l’eccesso di rendimento incrementale che ci si aspetta dal fondo, si deve far leva all’eccesso di rendimento di mercato superiore o inferiore al grado di esposizione al rischio di mercato intrinseco al titolo. Il CAPM Beta rappresenta il grado di esposizione al rischio di mercato.

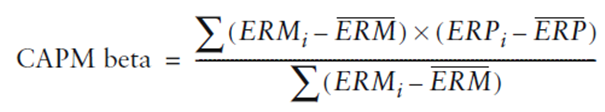
Fonte: Investment Performance Measurement (Bruce J. Feibel)

dove ERM corrisponde agli extra rendimento del mercato benchmark e ERP corrisponde ai rendimenti in eccesso del fondo. Il CAPM Beta è uguale alla covarianza degli extra rendimenti del fondo e del benchmark diviso per la varianza degli extra rendimenti del benchmark.

Osservazione 19> Il CAPM Beta misura in altre parole il grado di variabilità nei rendimenti del fondo attorno al rendimento medio del fondo, che è correlato con il grado della differenza dei rendimenti di mercato rispetto al rendimento medio di mercato. Questo coefficiente viene calcolato allo stesso modo della regressione Beta, ma distingueremo il CAPM Beta dalla regressione Beta in quanto stiamo relazionando i rendimenti di fondo in eccesso ai rendimenti di mercato in eccesso, invece di utilizzare i totali rendimenti di mercato e del fondo.

3. aggiungendo il rendimento di mercato al rendimento non rischioso in eccesso facendo leva sul CAPM Beta è possibile ricavare il rendimento atteso del fondo (il rendimento che mediamente ci si attende di ottenere):

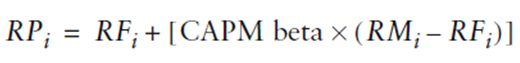
Fonte: Investment Performance Measurement (Bruce J. Feibel)

Osservazione 20> Quella scritta sopra è l’equazione del CAPM. Essa può essere interpretata affermando che i rendimenti di fondo dovrebbe essere uguale al tasso non rischioso più il premio per il rischio, in cui il premio per il rischio è calcolato guardando alla quantità con la quale i rendimenti del fondo variano in proporzione alla variabilità nel rendimento di mercato evidenziato.

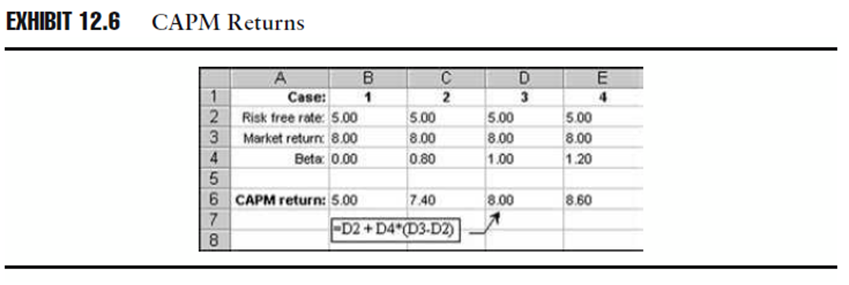
Lo schema 12.6 chiarisce l’utilizzo del CAPM con diversi scenari. In questi esempi, il tasso non rischioso è pari al 5% e il rendimento di mercato è uguale all’8%:

Nel primo caso il Beta del fondo è uguale a 0, indicando che i rendimenti di questo titolo non solo legati alla variabilità nei rendimenti del portafoglio di mercato; usando il CAPM, se Beta è uguale a 0, il rendimento del fondo dovrebbe essere uguale al tasso non rischioso, o 5%.
Nel caso 2, Beta del fondo è uguale a 0,8, indicando che -quando il Beta inferiore a 1 il titolo si dice difensivo– il rendimento del fondo è inferiore a quello dato dal rischio di mercato, ma i rendimenti del fondo si muoveranno sostanzialmente in linea con i rendimenti di mercato; quando i rendimenti di un fondo variano con magnitudo inferiore rispetto ai rendimenti di mercato il CAPM calcola un rendimento inferiore al rendimento di mercato, e il titolo sarà ancora relazionato alla volatilità; il rendimento dovrebbe essere quindi più alto rispetto al tasso non rischioso. Nel nostro esempio il rendimento è 7,40%.
Il caso 3 rappresenta un fondo con una Beta uguale a 1; se il fondo ha rendimenti che variano con lo stesso grado dei rendimenti benchmark, Beta è uguale a 1. Il rendimento calcolato dal CAPM in cui Beta è uguale a 1 dovrebbe essere uguale al rendimento di mercato, o 8%.
Il Beta del fondo nel caso 4 è uguale a 1.2. Una Beta maggiore di uno indica che –il titolo si dice aggressivo– la volatilità del mercato è stata maggiorata nel momento in cui viene riflessa nel fondo. Con il CAPM, una volatilità maggiore rispetto al mercato merita rendimenti maggiori e il rendimento di questo fondo corrisponde a 8,60%. Usando il CAPM il Beta amplifica anche i rendimenti al ribasso: un fondo con una Beta maggiore di 1 subisce perdite superiori rispetto al mercato quando anche quest’ultimo è al ribasso (bear market vs bull market).

Fonte: Investment Performance Measurement (Bruce J. Feibel)

Osservazione 21> Se il Beta è negativo quando i rendimenti del mercato scendono quelli del mercato salgono e viceversa. Il titolo si dice super difensivo o assicurativo (una sorta di assicurazione contro il rischio che il mercato scenda): titoli a beta negativo sono molto utili per diminuire il rischio di portafoglio contribuendo alla diversificazione.

Il foglio Excel illustra il calcolo di Beta del nostro fondo di riferimento. Il fondo ha un Beta pari 1, indicando che il fondo non ha rischi di mercato addizionali rispetto a quelli indotti dal benchmark. Dato una Beta di 1, il CAPM “prevede” un rendimento del fondo medio mensile uguale al rendimento di benchmark, o 1,98% (0,42% + 1 x (1,98% – 0.42%)).

Osservazione 22> Il CAPM è stato originariamente sviluppato da William Sharpe (ed anche indipendentemente da Lintner, Mossin e Trynor) partendo dal lavoro pionieristico della moderna teoria di portafoglio di Harry Markowitz e James Tobin. Il modello è stato poi soggetto di diversi test per determinare la sua validità rispetto ai dati del mondo reale e si sono succedute diverse proposte di estensione e variazione. I modelli multi fattore (vedi Arbitrage Pricing Theory) estendono il modello d’indice di mercato (o single index market model) per determinare le influenze dei rendimenti del manager su quelli predetti dal CAPM (vedi modelli: Treynor-Mazuy, 1966; Elton, Gruber, and Blake ,1996 and Gruber, 1996; Chen, Roll and Ross’s model, 1986; Fama and French, 1996; Fama-French-Carhart 1997). Nonostante ci sia questa sperimentazione e la susseguente evoluzione, il modello originale di regressione lineare di un singolo fattore continua ad essere lo strumento più usato per valutare la performance risk adjusted.

Indice di Treynor

Osservazione 23> Un’applicazione del CAPM Beta la si trova nel calcolo dell’indice di Treynor, che misura il rendimento in eccesso del tasso non rischioso diviso per il Beta. L’indice di Treynor può essere usato per classificare l’appetibilità di un particolare titolo in combinazione ad altri titoli, in cui parte del rischio totale intrinseco alla deviazione standard viene diversificata aggiungendo un adeguata composizione dei titoli in portafoglio.

Il modus operandi del calcolo è lo stesso modo dell’indice di Sharpe, eccetto che il Beta sostituisce la deviazione standard a denominatore. Sostituendo la deviazione standard con Beta, stiamo sostituendo la misura del rischio totale con la misura di mercato o rischio di sistematico (relativo al mercato/bechmark).

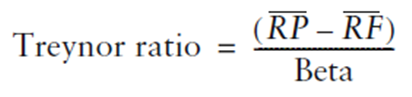
Fonte: Investment Performance Measurement (Bruce J. Feibel)

Alpha di Jensen

Il rendimento medio del fondo di riferimento (2,35%) è maggiore a quello generato dall’equazione CAMP (1,98%), mostrando che il nostro fondo ha un miglior rischio e una migliore efficienza di rendimento rispetto a quanto indicato dal CAPM.

Osservazione 24> È possibile ipotizzare che questa differenza sia dovuta alla gestione attiva del fondo dal manager del portafoglio, selezionando ad esempio titoli che sono sotto prezzati dal mercato. Potremo poi prendere l’ampiezza di questa sovra performance come informazione preziosa, visto che ciò rappresenta il valore aggiunto al benchmark, ma su base rettificata per il rischio -o risk adjusted-. E’ possibile utilizzare CAPM per isolare questa sovra performance aggiungendo un coefficiente addizionale, CAMP Alpha, al lato destro dell’equazione CAMP.

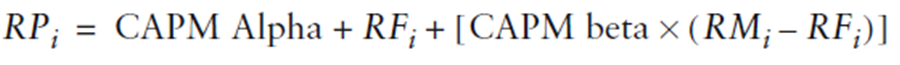
Fonte: Investment Performance Measurement (Bruce J. Feibel)

In questa sede il rendimento di fondo equivale al tasso non rischioso più il premio per il rischio, il tutto sommato al CAPM Alpha.

Osservazione 25> Il CAPM Alpha, o Alpha di Jensen, è il fattore di rendimento che non spiega la porzione di rendimenti “prevista” dal CAPM. L’Alfa di Jensen è frequentemente usata come misura del rendimento rettificato per il rischio maturato dal portafoglio. Michael Jensen sviluppò questa estensione al CAPM come uno strumento empirico-operativo per valutare i fondi dei manager. L’equazione CAPM rettificata può essere manipolata algebricamente per darle la forma di regressione lineare.

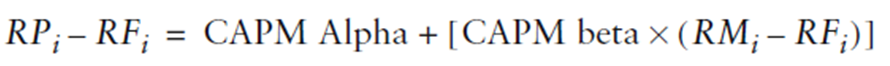
Fonte: Investment Performance Measurement (Bruce J. Feibel)

Osservazione 26> Questa equazione di regressione è la stessa dell’equazione di regressione del precedente articolo (vedi all’inizio), eccetto che noi rendiamo indipendente la variabile dei rendimenti di mercato in eccesso e dipendente la variabile dei rendimenti di fondo in eccesso. Sottraendo il rendimento di mercato in eccesso su cui si è fatta leva dal lato sinistro, ci dà la formula per calcolare l’Alfa di Jensen

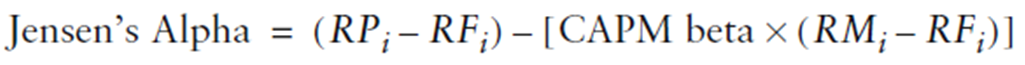
Fonte: Investment Performance Measurement (Bruce J. Feibel)

L’Alfa di Jensen calcolato nel foglio Excel del nostro fondo di riferimento è di 0,3675. Interpreteremo questo come la performance dello 0,37% del rendimento medio mensile positivo oltre a quello implicato dalla quantità di rischio di mercato considerato nel periodo.

Osservzione 27> Alfa è la misura della performance rettificata per il rischio di un fondo; può essere interpretata come il valore aggiunto dall’effettiva gestione del fondo e rettificato per il rischio. Se Alfa è maggiore di 0, il fondo avrà un rendimento maggiore di quello previsto da CAPM. I portafogli con un’Alfa di Jensen positiva giaciono sopra alla linea capital market line (Vedi: Capital Asset Pricing Model: il primo modello di mercato per il calcolo dell’adeguata remunerazione del rischio ed il pricing di titoli azionari). Un’Alpha di Jensen elevata indica rendimenti in eccesso dopo il controllo effettuato sulla sensibilità del mercato (Beta) del portafoglio: più Alfa è grande, migliore sarà la performance risk adjusted del manager date le ipotesi di CAPM. Un’Alpha di Jensen negativa indica che il fondo ha sottoperformato rispetto al rendimento atteso dal CAPM e quantificato mediante il rischio di mercato considerato.

Alfa si calcola con la stessa periodicità dei rendimenti evidenziati. Alfa si esprime comunemente in equivalenti annuali. L’Alfa media annua è la media mensile dell’Alfa per il numero dei periodi per anno.

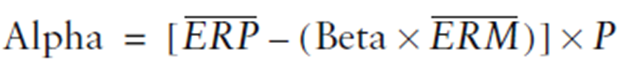
Fonte: Investment Performance Measurement (Bruce J. Feibel)

L’Alfa media annua del nostro fondo è 0.3675% x 12 = 4.41%.

I portfolio manager sono frequentemente giudicati in base alla loro abilità di aggiungere ‘Alpha’ (abilità di Stock Picking).

Osservazione 28> Un problema con l’Alpha è che può assumere accezioni differenti: a volte Alfa viene usata nel modo con cui noi abbiamo descritto il Valore Aggiunto, ossia la differenza tra il rendimento di fondo e quello di benchmark; usata in questo modo Alpha misura la sovra/sotto performance non rettificata per il rischio considerato. Sia la regressione Alpha sia l’Alfa di Jensen rettificano (aggiustano) per il rischio considerato, facendo leva sul rendimento di mercato maggiore o inferiore rispetto al Beta. Ma a volte l’Alpha o la Beta di un fondo vengono riportate senza spiegare se le rispettive misure sono state calcolate usando un’analisi di regressione dei rendimenti o usando un’equazione CAPM con input di eccesso di rendimento. Visto che i coefficienti di regressione e di CAMP hanno valori e interpretazioni diverse, è importante differenziarli quando stiamo calcolando o riportando statistiche di rischio. I coefficienti di regressione sono descrizioni statistiche di rendimenti attesi dai portafogli dato un rendimento di mercato, come rappresentati dal benchmark. Il rendimento del CAMP e il coefficiente Alfa sono stime teoriche di rendimenti attesi e eccessi di rendimenti dovuti dalla gestione del fondo.

Lo schema 12.8 riassume le diverse definizioni di Alfa.

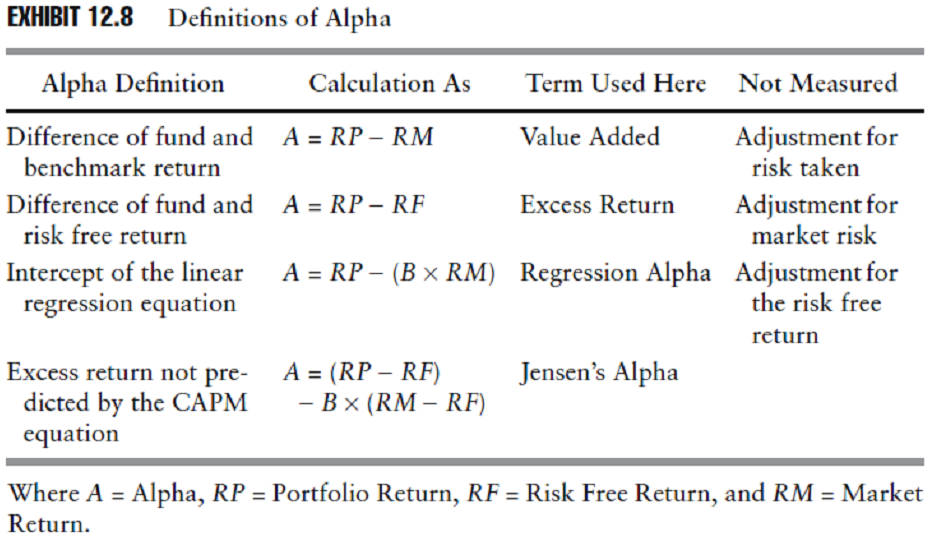
Fonte: Investment Performance Measurement (Bruce J. Feibel)

Nella proseguo della trattazione analizzeremo alcune misure di rendimento rettificate per il rischio utili quando il rischio viene misurato come perdita o come benchmark relativo al rischio assunto dal manager.

Il prossimo argomento a seguire dopo il relative risk adlusted return esamina invece come è possibile utilizzare la serie storica di un rendimento, assieme al rischio composito e le statistiche del rendimento, per quantificare la bravura, o skills, di un porfolio manager.

Come sempre, spero di aver riportato tutti i calcoli con cura, avendo preso a riferimento la più volte sopra citata fonte.

6) Absolute Risk Adj Ret (CAPM, M^2)