Nella precedente trattazione abbiamo trattato, analizzato e calcolato il valore aggiunto del rendimento del fondo rispetto al benchmark (Vedi: Valore aggiunto rispetto al benchmark. Cosa è. Come funziona.) per valutare il rendimento –corretto per il rischio (è fondamentale!)– prodotto dalla strategia attiva del manager: questo rendimento deve essere tale da coprire le spese di gestione e commissioni varie, oltre a risultare ancora in grado di battere il benchmark.
Osservazione1> Una delle ragioni principali del misurare -nel suo unicum- il rendimento rettificato per il rischio è utilizzare le statistiche di performance per differenziare i manager del fondo in base alla dimostrazione delle loro capacità di gestione dei portafogli nel passato. È possibile definire la capacità del portofolio manager come l’abilità di ricavare il valore aggiunto sul benchmark nel tempo (calcolata) in maniera meramente statistica (le skills ontologicamente riguardanti il manager sono lo stock picking ed il market timing). Verranno quindi differenziate le capacità dalla ‘fortuna’.
In questa trattazione si analizza nella maniera più semplice possibile come si possa usare le misure di rendimento, il rischio ed il rendimento rettificato per il rischio trattati nelle precedenti analisi, in modo da aggiungere input quantitativi al processo di valutazione dei manager del portafoglio.
Utilizzare il rischio ed il rendimento per valutare le skill del portfolio manager
I dati di misurazione della performance storica non forniscono una misura diretta della capacità: in un singolo periodo, il 50% dei manager raggiungerà più del rendimento mediano mentre l’altro 50% ne guadagnerà meno. Non è possibile affermare molto sul fatto che il manager raggiunga una performance superiore nel singolo periodo, perché è solo un’osservazione.
Osservazione 2> Occorre osservare la performance di molti periodi, e se il manager sovraperformerà regolarmente forse si potrà affermare che esiste una prova della capacità del Manager. Qui viene pertanto affrontato il problema dovuto alla probabilità dell’esistenza di un manager su 20 che apporterà sistematicamente valore aggiunto sul benchmark in un numero di anni prestabilito. E’ quindi difficile differenziare tra la capacità e la fortuna.
Anche se si è inclini ad accettare il fatto che è possibile dedurre la capacità quando non è presente, rimane sempre il problema di avere raramente la quantità desiderata di osservazioni storiche necessarie per valutare la performance.
Osservazione 3> Se si considera un anno come il singoli periodo più breve possibile su cui vogliamo valutare la performance di un manager, si ha bisogno di molti rendimenti annuali per isolare statisticamente la capacità dalla fortuna; se si accorcia il periodo di misurazione a trimestri o mesi, introduciamo artificialmente l’orizzonte a breve termine in una situazione in cui sono i risultati a lungo termine che interessano. Sia l’ampiezza media del valore aggiunto periodico sia il numero di periodi sopra i quali abbiamo osservazioni di rendimento determinano se sia possibile isolare statisticamente la capacità e fortuna.
Oltre al solito avvertimento che la performance superiore passata non è garanzia delle capacità future, possiamo utilizzare le misure delle performance storiche per provare a capire se il manager ha la capacità effettiva di gestire un portafoglio.
Osservazione 4> La misurazione della capacità si riferisce alla valutazione quantitativa della performance passata per avere una “prova statistica” della capacità passata, dati i limiti dei dati storici. Insieme all’informazione più qualitativa e all’informazione rivolta al futuro (cd forward looking), come le informazioni che riguardano i cambiamenti del manager, di stile d’investimento ecc, la misurazione della performance viene utilizzata nella valutazione e selezione dei manager d’investimento.
Ci sono diverse modalità di utilizzo del rendimento, del rischio e dei rendimenti rettificati per il rischio nella valutazione delle capacità passate. In questa sede daremo uno sguardo alla misurazione del valore statistico del valore aggiunto, in aggiunta alle altre modalità di disamina della consistenza del valore aggiunto dato dal manager.
Significatività statistica del valore aggiunto
Ora si passa ad isolare il valore aggiunto dalla gestione effettiva sottraendo il rendimento del benchmark periodico dai rendimenti del fondo. La media del valore aggiunto sul periodo fornisce un’indicazione riguardante la direzione e l’ampiezza del valore aggiunto; se il valore aggiunto è sia positivo sia ampio nel periodo, è possibile considerarlo come un’indicazione della capacità del manager.
Osservazione 5> E’ possibile quantificare se il valore aggiunto sia o statisticamente significativo o meno calcolando la t-statistic del valore aggiunto, ossia uno strumento utilizzato nella branca della statistica conosciuta come statistica inferenziale. I test statistici inferenziali calcolano una statistica basata sui dati che sono stati raccolti, in cui la statistica può essere usata per dedurre la forza nella relazione tra le variabili. Per esempio, noi siamo interessati a sapere se il valore aggiunto dal manager è o no statisticamente differente da 0. Per determinare questo stabiliremo un’ipotesi nulla che il manager non ha aggiunto valore sul periodo; l’ipotesi alternativa è che il manager ha aggiunto valore e poi si utilizzerà la t-statistic per cercare di provare che l’ipotesi nulla sia falsa.
La t-statistic è calcolata dall’equazione sotto riportata. Si divide la media del valore aggiunto per la deviazione standard del valore aggiunto, che è divisa a sua volta per la radice quadrata del numero delle osservazioni.

Il foglio 1 di Excel è un esempio di calcolo della t-statistic del valore aggiunto del nostro fondo di riferimento, che corrisponde a 0,69.
L’interpretazione della t-statistic dipende, come detto, dal numero delle osservazioni usate e dal livello di significatività scelto. Tale livello di significatività è il livello di tolleranza per affermare le capacità del manager, che potrebbe anche non avere. In pratica viene solitamente scelto il livello del 5% e la t-statistic associata richiesta per rifiutare l’ipotesi nulla -quella che afferma che il valore aggiunto è statisticamente indifferenziato da 0- è approssimativamente pari a 2 deviazioni standard (più precisamente circa 1,96 volte la deviazione standard), dipendendo inoltre dal numero delle osservazioni.
Osservazione 6> Dato che non è maggiore non possiamo rifiutare l’ipotesi nulla che il valore aggiunto è statisticamente diverso da 0. La t-statistic lavora attraverso il confronto tra il valore aggiunto e quello che possiamo aspettarci di osservare date le deviazioni standard del valore aggiunto. Se la t-statistic è alta abbastanza da rendere improbabile osservare le deviazioni casualmente, possiamo rifiutare l’ipotesi nulla e accettare che il manager abbia aggiunto valore sul periodo.
Se il fondo ha sovreperformato il benchmark ad un maggior grado in un brevi periodi o si hanno molte più osservazioni dello stesso valore aggiunto relativo, possiamo raggiungere una t-statistic che ci permette di rifiutare l’ipotesi nulla.
Osservazione 7> La t-statistic è strettamente correlata all’information ratio. Si potrebbe prendere l’information ratio e moltiplicarlo per la radice quadrata del numero delle osservazioni e guardare il risultato nel t-table per determinare se il valore aggiunto è statisticamente rilevante.
Consistenza del valore aggiunto
Esistono diversi problemi con la valutazione della performance presentate finora. In primo luogo è stato dato uno sguardo al valore aggiunto prodotto sul periodo di tempo senza considerare la consistenza della media del valore aggiunto. Si ipotizzi ad esempio di ri-valutare la performance del manager dopo diversi mesi addizionali in cui il manager batte drammaticamente il benchmark; questo aumenterebbe il valore aggiunto statistico e darebbe forse valore al t-statistic. In seguito, nel trimestre successivo, il manager potrebbe produrre una performance terribile e le conclusioni disegnate dalle statistiche cambierebbero.
Osservazione 8> Questo esempio si riferisce alla non stazionarietà: le statistiche che vengono calcolate sono stazionarie se rimangono stabili nel tempo; inoltre, si potrebbe essere interessati alla performance del manager dei singoli periodi più lunghi di un mese o di un trimestre. Si supponga ad esempio di valutare la performance di tre tipi di manager, ognuno con una comprovata esperienza di 5 anni; si hanno quindi a disposizione 20 trimestri di rendimenti per ogni manager.
Il foglio 1 di Excel mostra i rendimenti trimestrali di 3 fondi in aggiunta ad un appropriato indice di mercato di 5 anni. Useremo questi dati per produrre gli esempi in questa sezione.
Osservazione 9> Un modo di dare un senso alla stabilità della performance è di guardare a come il fondo apporta regolarmente valore aggiunto al benchmark. Un modo veloce per fare ciò è compiere il runs test, utilizzato per decidere se il valore aggiunto al benchmark, o ad altre statistiche, è il risultato di processi casuali o prove di sistematicità.
Procedimento operativo>
- Calcolare prima il valore aggiunto al benchmark per ogni periodo.
- Poi si evidenzia ogni periodo a seconda se possiede o no un valore aggiunto sul periodo: tale calcolo viene fatto per ogni periodo assegnando ‘1’ ai periodi che hanno un valore aggiunto sul benchmark, e uno ‘0’ ai periodi che non lo possiedono.
- successivamente si cerca la prova della regolare performance sul benchmark. E’ possibile fare questo analizzando i run dei dati, ossia i periodi in cui esiste un andamento di fondo (trend) del valore aggiunto. Ciò è simile a cercare periodi in cui una serie di lanci di medaglie cadono regolarmente su testa o croce. Se i valori nella colonna J sono gli stessi da un trimestre all’altro, c’è un run. Quando i risultati cambiano da un trimestre all’altro allora ci sarà una rottura dei run. Le colonne dalla N alla P indicano i run con una ‘N’ e le rotture dei run con una ‘Y’.
- Si contano il numero delle rotture nei run. Se il modello del valore aggiunto fosse casuale, ci si attenderebbe la metà dei mesi che si invertono (se ci fossero periodi con regolare valore aggiunto, ci aspetteremo un minor numero di capovolgimenti).
- Si può dividere il numero dei run per il numero possibile di run al fine di ricavare il ratio dei run: un processo casuale restituirebbe un indice di run riguardante i run attesi dello 0,5; un indice vicino a 0 indicherebbe che c’è un pattern nell’andamento di fondo del valore aggiunto. Nonostante un indice vicino a 1 indichi che non ci sono andamenti, il processo non sarebbe interamente casuale.
In questa sede il focus si rivolge ai fondi con un indice vicino a 0. Qui il fondo B ha il miglior indice di run.
Analisi Rolling Period
Osservazione 10> Un problema del run test, chiamato in causa come metrica della consistenza della performance, è che indica solo se è presente o meno un valore aggiunto ma non l’ampiezza dello stesso. Si possono ad esempio usare le misure dei rendimenti rettificati per il rischio per cercare sia la prova dell’esistenza sia dell’ampiezza della performance ritenuta consistente e sistematica.
Prima si calcolano le maggiori statistiche del rischio, del rendimento e del relativo rendimento rettificato per il rischio per il periodo nel foglio di calcolo sottostante. Nello schema qui sotto si può vedere che i fondi B e C dominano il fondo A sotto ogni punto di vista, con un alto rendimento, valore aggiunto e Information ratio e con anche deviazioni standard e deviazioni al ribasso più basse.

Fonte: Investment Performance Measurement (Bruce J. Feibel)
L’unica scelta è selezionare i fondi B e C: questi fondi hanno sovraperformato il benchmark con simili deviazioni standard. Il fondo C ha un rendimento più elevato, una deviazione standard più bassa e un’Information ratio più alto; tuttavia la scelta non è totalmente palese, perché il fondo B mostra una deviazione al ribasso più bassa se questa è un criterio importante nella nostra selezione del manager.
Osservazione 11> Prima di prendere decisioni, il focus si concentra sul valutare la consistenza dei manager circa queste statistiche. Avendo in mente un orizzonte valutativo di un anno e con 5 anni di dati, potremo calcolare 5 calendari annuali di rendimenti cumulativi, deviazioni standard e ricavare i rendimenti rettificati per il rischio.
Il foglio 2 schema 1 mostra il rischio annuale e le statistiche di rendimento per ogni manager.
Guardando alle statistiche di periodi più piccoli, è possibile dare un senso alla variabilità nella classifica relativa dei fondi nel periodo. Nello schema del foglio due sotto si vede che il fondo C ha un maggiore Information ratio in 3 degli ultimi 5 anni.
Osservazione 12> Se si avessero più fondi a disposizione da selezionare, potremmo eseguire questa analisi usando statistiche di classificazione e di ordine (vedi, per più informazioni: Relative Return, ranking e peer group analysis. Cosa sono e quali misure si utilizzano.) per vedere quanto regolarmente ogni manager è classificato nel primo quartile dei manager, e così via.
Osservazione 13 > Quando si misura la performance di un manager solitamente ci si riferisce a periodi lunghi di tempo, ma non ad un periodo di tempo sufficientemente lungo per determinare se la performance abbia apportato o meno un valore sufficiente al benchmark. Possiamo aggiungere quindi al numero delle osservazioni e costruire un’analisi più consistente eseguendo un’analisi rolling period.
Osservazione 14> In una rolling period analysis si calcolano statistiche in “finestre fisse di tempo”, dove con ogni nuova osservazione aggiungiamo un nuovo periodo facendo “rollare” il periodo precedente. Per esempio, invece di calcolare Information ratio annuali basati su 5 anni di cui si posseggono dati, possiamo infatti calcolare 17 Information ratio annuali con 20 trimestri di dati. Si inizia con il primo trimestre in cui si hanno i dati dei primi 4 trimestri e si calcola l’Information ratio di ogni trimestre successivo a quello, aggiungendo il trimestre più recente e facendo cadere quello precedente.
Il foglio 3 mostra come possiamo analizzare la performance su base rolling.
Procedimento operativo>
- Qui è stato fittiziamente calcolato un Information ratio di ogni trimestre iniziando dal quarto trimestre del 1996; questo trimestre è il primo dei 4 trimestri di dati a disposizione, inclusi il trimestre corrente e i tre precedenti che non sono mostrati.
- In seguito, nel primo trimestre del 1997 calcoleremo un nuovo Information ratio che include i rendimenti dal primo trimestre del 1997 e che esclude, invece, i rendimenti dal primo trimestre del 1996. Facciamo ciò per ogni periodo fino al periodo corrente per ricavare la serie di periodi di rollio degli Information ratio.
È possibile utilizzare questi dati in diversi modi:
- in primo luogo, guardando alla consistenza della classificazione dei 3 fondi nel tempo.
- in secondo luogo è possibile vedere che esiste un trend definito all’inizio del periodo in analisi, con inizialmente i fondi A e C dominanti, e poi i fondi C e B dominanti per un altro periodo.
- infine, nel periodo più recente non ci sono trend chiari visto che la classificazione si è modificata diverse volte.
Nello schema qui sotto si vede come è possibile dare un senso migliore alla performance relativa del manager usando un grafico a linee.
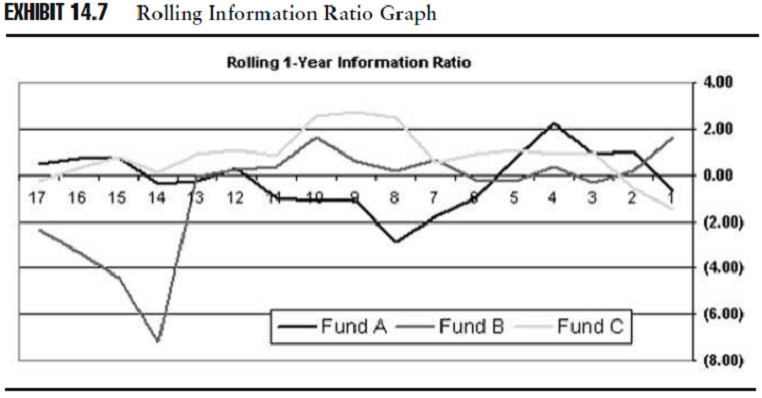
Fonte: Investment Performance Measurement (Bruce J. Feibel)
Osservazione 15> Oltre a fornire alcune informazioni, come la performance relativa dei manager, la rolling period analysis fornisce anche informazioni su come mettere le performance in prospettiva. Per esempio, l’Information ratio annuale del fondo B nel terzo trimestre del 1997 (14 periodi fa) è una deviazione estrema. Occorrerebbe discutere della situazione con un manager e vedere se escludere dall’analisi quei periodi per capire meglio le ragioni della performance del periodo; altrimenti si può decidere che quel periodo è più rappresentativo della performance attesa del manager su un particolare ciclo di mercato dando più enfasi al periodo nell’analisi di performance. Potrebbe anche essere interessante guardare più da vicino la recente performance del fondo C. Anche se questo fondo ha una comprovata esperienza di 5 anni, non è attrattivo come nei periodi più recenti.
Si può dare un ulteriore sguardo alla performance creando un grafico che tracci il movimento nel periodo di 1 anno del tracking error contro al valore aggiunto su base rolling: queste sono le due variabili che compongono l’Information ratio. Questo tipo di grafico è a volte chiamato ‘sentiero a chiocciola’ (vedi schema sotto).

Fonte: Investment Performance Measurement (Bruce J. Feibel)
Includendo il periodo di tempo sopra il quale si verifica l’osservazione, aggiunge valore tracciando semplicemente le statistiche di rendimento e di rischio. Per esempio, qui vediamo che il valore aggiunto oscillante è sceso mentre la rilevazione dell’errore aumenta negli ultimi periodi.
Conclusioni
In questa analisi, coerentemente alle precedenti trattazioni, sono state fornite alcune (non tutte) metriche per valutare se un portfolio manager abbia una gestione attiva in grado di aggiungere sistematicamente -ossia in maniera robusta statisticamente parlando- valore al benchmark. In altre parole si cerca di isolare la fortuna dalle reali abilità del manager che, a loro volta, dovrebbero giustificare l’esistenza di fondi a strategie attive.
Sono state inoltre riportate alcune statistiche di performance per integrare, nella presente trattazione, le precedenti analisi circa le metriche di performance di fondi comuni d’investimento.
Come sempre, mi scuso della rozzezza della presentazione in Excel e spero di non aver fatto figuracce con i calcoli.
Your Best
DF