Nell’analisi e nella valutazione di un trading system su qualunque strumento (che si tratti di Futures, Opzioni o Forex), il concetto di expectancy è quello di cui facciamo più largo utilizzo (magari non sempre consapevolmente). Numericamente l’expectancy altro non è che l’average trade, ma a livello concettuale, la sua costruzione ci offre spunti interessanti su cui lavorare.
Expectancy, Average Trade e sostenibilità di una Strategia
La virtù del calcolo dell’expectancy sta nel fatto che in un unico valore vengono combinate alcune informazioni molto importanti circa l’opportunità di sostenere un certo investimento: la probabilità che questo investimento vada a buon fine e la relazione che questa probabilità instaura con la remunerazione del rischio sottesa a tale investimento.
In particolare questa relazione è definita come segue:
E = W x P(W) – L x P(L)
Dove W è il profitto medio delle operazioni vincenti, L quello delle operazioni perdenti e P(W) e P(L) le rispettive probabilità di realizzazione.
Nella realtà dei trading system questo valore è incalcolabile in quanto nessuno degli elementi detti è noto. Ciò che abbiamo a disposizione, infatti, non è l’insieme di tutti i trade che il sistema ha generato e genererà (che sarebbe idealmente necessario per calcolare il valore corretto di E), ma il suo sottoinsieme dei trade prodotti nell’arco di tempo analizzato dal backtest.
Questa approssimazione è l’origine dell’uguaglianza con l’average trade, che per definizione è calcolato su tale sottoinsieme. Potremmo dire che l’average trade è una stima dell’expectancy del sistema: maggiore la numerosità del campione (quindi il numero dei trade), maggiore la precisione della stima.
L’impossibilità di calcolarla con precisione rende il concetto di expectancy inutilizzabile nel trading? Non del tutto: vediamo il perché.
Parlando di expectancy, l’ambito che più ne semplifica la comprensione è, purtroppo, quello meno adeguato quando si parla di trading e investimenti: il gioco d’azzardo.
Prendiamo, ad esempio, la roulette francese, con due possibili scommesse: quella sul colore, e quella sul numero singolo, e calcoliamone l’expectancy.
La scommessa sul colore
Ci sono 18 caselle rosse, 18 caselle nere e una casella verde. In caso di vittoria la scommessa è pagata con un incremento della nostra equity pari al valore a rischio, mentre in caso di sconfitta, l’equity si riduce di un’entità pari all’importo rischiato.
Poniamo, ad esempio, che l’ammontare della scommessa sia di 1€, e di puntare sul rosso. Per calcolare le probabilità di vittoria si usa il seguente approccio: si prende il numero di casi che ci fanno vincere e si guarda che porzione rappresentano del totale dei casi possibili.
Nel nostro caso:

La probabilità di perdere invece sarà uguale a tutti i casi restanti, ovvero 100% – 48.6% = 51.4%.
La vittoria, come abbiamo detto vale 1€, e la sconfitta -1€. Quindi l’expectancy è:
E = 1 × 48.6% −1 × 51.4% = −0.027€
Questo valore, -0.027€, va interpretato come l’ammontare vinto o perso (in questo caso perso) ogni volta che decidiamo di scommettere. Fondamentalmente è l’average trade del gioco della roulette.
L’enorme importanza di questo valore, tanto per il giocatore d’azzardo quanto per lo sviluppatore di trading system, deriva dalla cosiddetta Legge dei Grandi Numeri.
La Legge dei Grandi Numeri, anche detta Legge Empirica del Caso, è quella legge che sembra imporre all’universo di far convergere le realizzazioni alle attese, a patto che venga effettuato un sufficiente numero di esperimenti.
Nel nostro caso la Legge dei Grandi Numeri suggerisce che più volte puntiamo (su rosso o sul nero) più ci avviciniamo alla certezza che avremo perso mediamente 0,027€ per ogni Euro scommesso. La dimostrazione è affidata al grafico di Figura 1, dove si osserva l’andamento del profitto medio della scommessa sul rosso all’aumentare del numero di giocate (asse orizzontale): la sua convergenza al valore atteso (negativo) non è solo evidente, ma è anche piuttosto rapida.
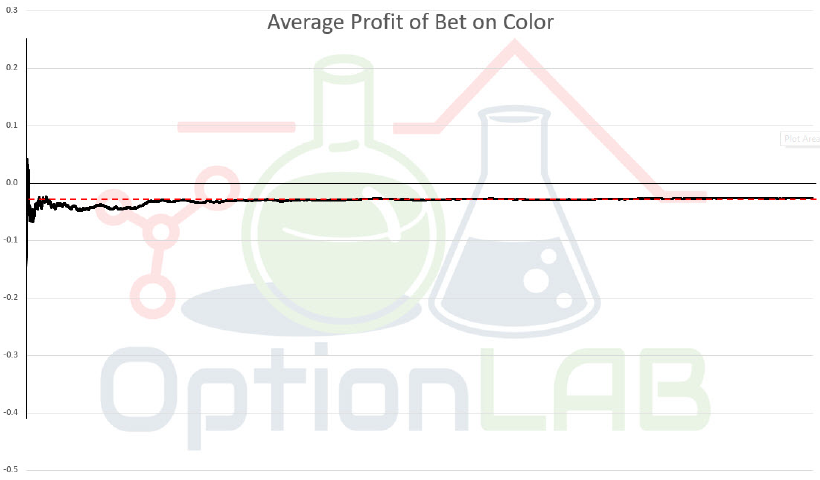
Figura 1: al netto di qualche shock iniziale, il rendimento medio della scommessa tende alla sua expectancy
L’expectancy non ci da alcuna indicazione sulla “rischiosità” dell’investimento
La scommessa sul numero singolo
Ripetiamo i conteggi appena effettuati, considerando però questa volta la scommessa sul numero singolo: 1 caso favorevole su 37, e una corrispondente vincita pari a 35 volte il rischio assunto.
L’expectancy è:
E = 1 × 48.6% −1 × 51.4% = −0.027€
Non dovrebbe sorprenderci ritrovare la stessa expectancy della scommessa sul colore.
Il gioco della roulette, per come è stato concepito, ha un’expectancy identica su ogni possibile puntata. Non importa su cosa, o con quale modalità voi scommettete, il casinò guadagnerà 2,7 centesimi di Euro per ogni Euro che voi scommettete, in media, sui grandi numeri.
Come mai allora, intuitivamente, noi percepiamo le due scommesse come così diverse tra loro?
La risposta sta nel rischio, che come detto l’expectancy non coglie.
La scommessa sul numero singolo è estremamente più rischiosa per il Casinò, perché l’equity che ne deriva è estremamente più volatile di quella ottenuta accettando le puntate sul colore. Possiamo confrontare le due equity in Figura 2.

Figura 2
Come si vede le due equity vanno nella stessa direzione: esse hanno infatti la stessa expectancy. Non vi è alcun dubbio, tuttavia, che l’equity della scommessa sul colore scenda in maniera molto più efficiente, lasciando meno margine al caso.
distribuite più o meno equamente. Nel caso della scommessa sul numero singolo, invece, si avranno 1 vittoria molto importante, e 36 sconfitte molto piccole tutte di seguito distribuite in due blocchi, come schematizzato in Figura 3.

Figura 3
Questa incertezza ai Casinò non piace, e per controllarla impongono limiti di puntata molto più bassi nelle scommesse con payoff più alti. La puntata massima sul numero singolo è solitamente dalle 5 alle 10 volte più piccola rispetto alla puntata massima sul colore, e non è un caso: la deviazione standard dei rendimenti delle scommesse sui numeri singoli, infatti, è 6 volte maggiore di quella sul colore.
Imporre limiti di puntata più restrittivi è una misura necessaria di controllo del rischio per il Casinò, ma che probabilmente fa “a malincuore”. Ridurre a un sesto la scommessa media, oltre a standardizzare il rischio tra le due scommesse, riduce però di fatto a un sesto l’expectancy del sistema “puntata sul numero singolo”, quindi il guadagno del Casinò.
Si può affermare, almeno sulla roulette, che i Casinò non guadagnano tanto sui numeri, ma sui colori.
Il risultato è che il portafoglio di un Casinò è allocato in maniera estremamente poco efficiente: per omogeneizzare il rischio sulle scommesse di cui è controparte, il banco è costretto a vincolare i giocatori a ridurre l’esposizione sulle scommesse più rischiose, sebbene abbiamo la stessa expectancy delle altre, riducendo così i suoi guadagni. Per trovare un’analogia con il trading, le sale da gioco sono costrette a utilizzare contemporaneamente strategie i cui profili di rischio/rendimento variano sensibilmente da una strategia all’altra. Se ne avesse la possibilità, il banco obbligherebbe tutti i giocatori a scommettere sulle giocate binarie, come rosso/nero o pari/dispari, ma l’esperienza di gioco ne risentirebbe, ed è quindi costretto a sacrificare (=investire) parte dei suoi rendimenti per rendere il gioco più emozionante (=rischioso) e attrarre dunque più clienti.
Cosa può modificare l’expectancy di un sistema? Non il Money Management. Nessuna tecnica di position sizing ha il potere di “migliorare” o “peggiorare” il profilo di rischio di un sistema di scommesse. Questo non vuol dire che non bisogna utilizzare logiche di dimensionamento della posizione, ma che da sole non possono essere la risposta alla domanda “come faccio a trasformare questo sistema mediocre in un buon sistema?”.
Solo lavorando sulla componente predittiva, possiamo variare l’expectancy del sistema!
Nella seconda parte dell’articolo, vedremo come isolare questa componente predittiva, e produrremo una dimostrazione di quest’ultima affermazione, mostrando come strategie grid di tipo martingala che non contengano alcuna componente predittiva (un “edge”, inteso come vantaggio), condividano lo stesso destino.
