Cren
Forumer storico
Non sapevo come contrassegnare questo thread, visto che al campo "Argomento" un bel "Programmazione R" non c'è, e allora ho messo "Programmazione Amibroker" visto che, tutto sommato, se ci sono in giro le librerie per interfacciarli, allora non dovrebbe essere un problema mettere in produzione il codice in quell'ambiente.
Stasera non esco, e quindi vi beccate questo tutorial
Cosa vogliamo fare?
Non so quanti di voi diano regolarmente un'occhiata alla matrice di covarianza (dubito) e di correlazione (più probabile) degli strumenti finanziari con cui lavorano; io lo faccio abbastanza spesso, non tanto perchè mi piaccia quanto perchè spesso mi serve come input per aiutarmi a decidere come suddividere il capitale tra vari strumenti.
Non so nemmeno quanto di voi sanno che passare da l'una all'altra non richiede alcun processo di stima sui dati, nè altre diavolerie: ce la si può cavare con un paio di operazioni tra matrici, che spiego nel seguito ma che poi deleghiamo ai software (per inciso lo fa anche Hoadley, quindi quello che espongo nel seguito si può benissimo replicare in Excel in tempi rapidi).
Se V è la matrice di covarianza, la matrice di correlazione P è semplicemente (ce la caviamo con la sigla dei supporti ottici per tenere la formula a mente )
)
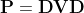 ,
,
Stasera non esco, e quindi vi beccate questo tutorial
Cosa vogliamo fare?
Non so quanti di voi diano regolarmente un'occhiata alla matrice di covarianza (dubito) e di correlazione (più probabile) degli strumenti finanziari con cui lavorano; io lo faccio abbastanza spesso, non tanto perchè mi piaccia quanto perchè spesso mi serve come input per aiutarmi a decidere come suddividere il capitale tra vari strumenti.
Non so nemmeno quanto di voi sanno che passare da l'una all'altra non richiede alcun processo di stima sui dati, nè altre diavolerie: ce la si può cavare con un paio di operazioni tra matrici, che spiego nel seguito ma che poi deleghiamo ai software (per inciso lo fa anche Hoadley, quindi quello che espongo nel seguito si può benissimo replicare in Excel in tempi rapidi).
Se V è la matrice di covarianza, la matrice di correlazione P è semplicemente (ce la caviamo con la sigla dei supporti ottici per tenere la formula a mente
 )
)dove D è un'altra matrice che adesso definiamo e il prodotto è ovviamente di tipo vettoriale e non scalare (niente paura! Fanno tutto i software!):
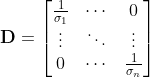 ,
,
le volatilità da sbattere sulla diagonale le prendete da V, naturalmente, ed ecco spiegato perchè si passa da una parte all'altra in un batter d'occhio.
Quindi, nel caso opposto, faremo l'operazione inversa: per passare dalla matrice di correlazione a quella di covarianza ci serve naturalmente P ma anche un vettore di volatilità.
Qualcuno avrà già capito dove voglio arrivare, quindi vengo al sodo: cosa succede se, passando dalla matrice di correlazione a quella di covarianza, il vettore di volatilità non è stimato sui dati storici ma proviene dai book delle opzioni (ovvero dalla volatilità implicita *generalmente* front month e interpolata ATM)?
Dal punto di vista matematico, non cambia una cippa: la matrice resta internamente coerente, e io non vi annoio con questi dettagli.
Dal punto di vista finanziario, tuttavia, sostituiamo una misura backward looking (la volatilità storica) con una forward looking (la volatilità implicita), con tutti i vantaggi del caso.
Il risultato è una matrice di covarianza ibrida: la varianza (cioè la diagonale principale) è squisitamente implicita, non guarda al passato; la covarianza deriva dalla volatilità implicita ma è "tarata" sulle correlazioni storiche.
Va da sè che questo oggetto risente in tempo reale di tutto ciò che accade nel book delle opzioni in prossimità dello spot, ma anche (mi sembra di essere Veltroni) di tutto ciò che accade al sottostante.
Nel commento ho scritto
Che me ne faccio?
...cominciare a dare questa matrice ibrida in pasto ad un portafoglio a varianza minima può riservare delle sorprese rispetto alla canonica covarianza storica stimata sui dati passati
Se interessa, posso mostrare il procedimento in Hoadley ma è tutto sommato molto facile da fare.
le volatilità da sbattere sulla diagonale le prendete da V, naturalmente, ed ecco spiegato perchè si passa da una parte all'altra in un batter d'occhio.
Quindi, nel caso opposto, faremo l'operazione inversa: per passare dalla matrice di correlazione a quella di covarianza ci serve naturalmente P ma anche un vettore di volatilità.
Qualcuno avrà già capito dove voglio arrivare, quindi vengo al sodo: cosa succede se, passando dalla matrice di correlazione a quella di covarianza, il vettore di volatilità non è stimato sui dati storici ma proviene dai book delle opzioni (ovvero dalla volatilità implicita *generalmente* front month e interpolata ATM)?
Dal punto di vista matematico, non cambia una cippa: la matrice resta internamente coerente, e io non vi annoio con questi dettagli.
Dal punto di vista finanziario, tuttavia, sostituiamo una misura backward looking (la volatilità storica) con una forward looking (la volatilità implicita), con tutti i vantaggi del caso.
Il risultato è una matrice di covarianza ibrida: la varianza (cioè la diagonale principale) è squisitamente implicita, non guarda al passato; la covarianza deriva dalla volatilità implicita ma è "tarata" sulle correlazioni storiche.
Va da sè che questo oggetto risente in tempo reale di tutto ciò che accade nel book delle opzioni in prossimità dello spot, ma anche (mi sembra di essere Veltroni) di tutto ciò che accade al sottostante.
Nel commento ho scritto
Codice:
[COLOR=DarkRed]# Visualizzo la nostra matrice ibrida: la correlazione tra gli asset è stimata a partire dai dati
# storici, ma varianza e covarianza derivano dalla volatilità implicita delle opzioni; ne segue che
# varianza e covarianza sono ora sensibili sia a quanto accade nel book delle opzioni sia a quanto
# accade al sottostante[/COLOR]...cominciare a dare questa matrice ibrida in pasto ad un portafoglio a varianza minima può riservare delle sorprese rispetto alla canonica covarianza storica stimata sui dati passati

Se interessa, posso mostrare il procedimento in Hoadley ma è tutto sommato molto facile da fare.
Codice:
[COLOR=Teal]# ******************************************************************************************************
# Matrice di covarianza ibrida: volatilità implicita - covarianza storica
# By Cren
# ******************************************************************************************************
# Il package 'rmgarch' non lo trovate su CRAN, va installato scaricandolo da R-Forge; con la prossima
# istruzione lo scarichiamo e lo installiamo[/COLOR]
install.packages("rmgarch", repos="http://R-Forge.R-project.org")
[COLOR=Teal]# Carico i package necessari; se ve ne manca qualcuno, potete scaricarli da qui:
# http://cran.r-project.org/web/packages/available_packages_by_name.html[/COLOR]
require(lavaan)
require(quantmod)
require(rmgarch)
require(timeSeries)
[COLOR=Teal]# Scarico da Yahoo quattro serie OHLC di ETF: S&P500, Treasury Long Term, oro e materie prime[/COLOR]
tickers <- c('SPY', 'TLT', 'GLD', 'DBC')
getSymbols(tickers, from = '1950-01-01')
[COLOR=Teal]# Raggruppo nella matrice 'X' i prezzi di chiusura degli ETF allineandoli e rimuovendo i dati mancanti[/COLOR]
X <- na.omit(merge(Cl(SPY), Cl(TLT), Cl(GLD), Cl(DBC)))
[COLOR=Teal]# Calcolo i rendimenti aritmetici[/COLOR]
dX <- returns(X, method = 'discrete') ; dX[1,] <- 0
[COLOR=Teal]# Specifico un modello EGARCH multivariato a residui normalmente distribuiti; potete vedere un elenco
# dei modelli supportati digitando '?ugarchspec' nella console[/COLOR]
spec <- gogarchspec(mean.model = list(model = 'constant'), variance.model = list(model = 'eGARCH'), distribution.model = 'mvnorm')
[COLOR=Teal]# Stimo la matrice di covarianza condizionata storica[/COLOR]
hist.V <- rcov(gogarchfit(spec = spec, data = dX))[,,nrow(dX)]
[COLOR=Teal]# Converto la matrice di covarianza nella corrispondente matrice di correlazione[/COLOR]
hist.Rho <- cov2cor(V)
[COLOR=Teal]# 'iv' è il vettore delle volatilità implicite front month che raccogliete dal mercato (presumibilmente
# una media pesata delle volatilità implicite At-The-Money); in questo esempio io le ho generate
# casualmente dalle volatilità storiche solo per avere un valore numerico abbastanza simile da usare,
# nella realtà andrete a prendere la IV ATM front month direttamente dal book delle opzioni[/COLOR]
iv <- diag(V) * exp(rnorm(length(diag(V)), mean = .2, sd = .4))
[COLOR=Teal]# Converto la matrice di correlazione nella corrispondente matrice di covarianza utilizzando, al posto
# delle volatilità storiche calcolate in precedenza, le volatilità implicite[/COLOR]
hybrid.V <- cor2cov(R = hist.Rho, sds = iv)
[COLOR=Teal]# Visualizzo la nostra matrice ibrida: la correlazione tra gli asset è stimata a partire dai dati
# storici, ma varianza e covarianza derivano dalla volatilità implicita delle opzioni; ne segue che
# varianza e covarianza sono ora sensibili sia a quanto accade nel book delle opzioni sia a quanto
# accade al sottostante[/COLOR]
hybrid.V
Ultima modifica:

 per l'impegno
per l'impegno